>	restart;#"m07_p22"

Se dispone de dos dispositivos cilindro-mbolo iguales, de 10 cm de dimetro, limitados superiormente por sendos mbolos de 5 kg inicialmente a 0,5 m del fondo. Uno est lleno de n-butano y el otro de n-heptano, ambos en equilibrio en un ambiente a 20 C. A partir de un cierto instante, se ponen en comunicacin y se empuja lentamente para que vaya pasando n-heptano al otro recipiente. Se pide:
a) Cantidades iniciales de sustancia.
b) Representacin esquemtica de los sucesivos estados en los diagramas p-x y T-x.
c) Demostrar que la lnea de liquidus en el diagrama p-x es una lnea recta.
d) Estado de equilibrio cuando el mbolo del n-heptano ha bajado 1 cm..

e) Posicin del mbolo del n-butano en el caso anterior. Que hubiera pasado si este mbolo hubiese estado anclado al cilindro?.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="C4H10":su2:="C7H16":dat:=[Di=0.1*m_,mE=5*kg_,T0=(273+20)*K_,L=0.5*m_,Lh=0.49*m_]:dat:=[op(dat),A=evalf(subs(dat,Pi*Di^2/4)),V1=evalf(subs(dat,L*Pi*Di^2/4))]:evalf(%,2);

Esquema:

>

>

Eqs. const.:

>

eqETg:=subs(eq1_11,eq1_12);eqEE:=eq1_16;for i from 1 to 2 do gdat||i:=get_gas_data(su||i);ldat||i:=get_liq_data(su||i);dat||i:=op(dat),Const,gdat||i,ldat||i,SI2,SI1;od:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:'rho1'=subs(dat1,rho),'rho2'=subs(dat2,rho);

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;

a)Cantidades iniciales de sustancia.

>	'T0'=subs(dat,T0);pv1_:=evalf(subs(Const,pv1(T0)));pv2_:=evalf(subs(Const,pv2(T0)));p1:=p0+mE*g/A;p1_:=subs(dat1,p1);Tv1_:=subs(dat,solve(p1_=pv1(T),T));Tv2_:=subs(dat,solve(p1_=pv2(T),T));

luego a 20 C el heptano es lquido y el butano gas.

>	n1:='p1*V1/(R[u]*T0)';n1_:=subs(dat1,n1);n2:=rho2*V1/M2;n2_:=subs(rho2=rho,M2=M,dat2,n2);

b) Representacin esquemtica de los sucesivos estados en los diagramas p-x y T-x.

>

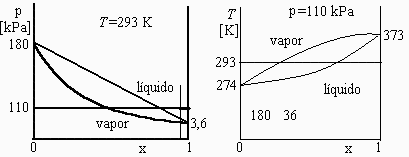
c) Demostrar que la lnea de liquidus en el diagrama p-x es una lnea recta.

>	'solve(subs(xv2=1-xv1,xl2=1-xl1,{eqE1,eqE2}))';sol1:=solve(subs(xv2=1-xv1,xl2=1-xl1,{eqE1,eqE2}),{xv1,xl1});

que ensea que para T=cte la xl1 vara linealmente con p.

d) Estado de equilibrio cuando el mbolo del n-heptano baja 1 cm.

En el de n-heptano queda:

>	n22:=rho*V1/M*(Lh/L);n22_:=subs(dat2,n22);

Luego en el mezclado queda:

>	n01_:=n1_:'butano_n01'=evalf(%,2);n02_:=n2_-n22_:'heptano_n02'=evalf(%,2);x02:=n02/(n02+n01);x02_:=n02_/(n02_+n01_);

que, como es casi todo heptano (76%), estar liquido y ocupar:

>	Vm:=n*vm;vm:=x2*M2/rho2+(1-x2)*M1/rho1;Vm_:=subs(x2=x02_,n=n01_+n02_,n*(subs(dat2,x2*M/rho)+subs(dat1,(1-x2)*M/rho)));L2:='Vm'/A;L2_:=subs(dat,Vm_/A);

Comprobacin de que esa fraccin molar de heptano es superior a la de liquidus:

>	Tv1p1_:=solve(p1_=pv1(T),T);Tv2p1_:=solve(p1_=pv2(T),T);T0_:=subs(dat,T0);sol2:=solve(subs(x02=xl2,x01=1-xl2,p=p1_,pv1=pv1_,pv2=pv2_,{eqNV,eqNL,eqC1,eqC2,eqE1,eqE2}),{xv1,xv2,xl1,xl2,xl0,xv0});

es decir, para que quedara bifsico tendra que ser 0,014 < x02_< 0,40.

e) Posicin del mbolo del n-butano en el caso anterior. Que hubiera pasado si este mbolo hubiese estado anclado al cilindro?.

Si el mbolo hubiese estado anclado, el volumen de la mezcla estara fijo y la presin bajara hasta quedar un equilibrio bifsico con (Vm=VmV+VmL=VmV+0):

>	eqVm:=V1=xv0*(n01+n02)*R[u]*T0/p;eqVm_:=subs(n01=n01_,n02=n02_,dat1,eqVm):sol3:=solve(subs(x02=x02_,x01=1-x02_,pv1=pv1_,pv2=pv2_,dat1,dat1,{eqNV,eqNL,eqC1,eqC2,eqE1,eqE2,eqVm_}),{xv1,xv2,xl1,xl2,xl0,xv0,p})[2]:subs(SI1,%);

i.e. la presin en el recipiente de la mezcla bajara hasta 35 kPa.

>