>	restart:#"m07_p17"

Con el fin de estimar el número de Avogadro a partir de la segregación de una mezcla coloidal por efecto gravitatorio, se ha preparado una muestra en un microscopioy se han realizado las siguientes medidas: la suspensión coloidal es de partículas sólidas de 0,45±0,1 µm de diámetro y 1255±10 kg/m3 de densidad en agua a 15±1 °C, y la densidad de partículas sólidas disminuye a la mitad cada 46±2 µm de altura. Se pide:

a) Establecer la relación entre la variación de la concentración y las densidades.

b) Estimar el número de Avogadro.

c) Estimar la incertidumbre en el valor anterior.

Datos

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":dat:=[Di=0.45e-6*m_,rho2=1255*kg_/m_^3,T=288*K_,Dz12=46e-6*m_]:dat:=[op(dat),op(subs(Const,dat,[SDD=.1e-6*m_/Di,Srhorho=evalf(10*(kg_/m_^3)/rho2),STT=evalf(1*K_/T0),Szz=2e-6*m_/Dz12]))];

Esquema:

>

>

Eqs. const.:

>	g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:

>	eqGD:=0=S*dT-V*dp+Sum(n[i]*dmu[i],i);

>	eqEq1:=T=cte;eqEq1:=dT/dz=0;eqEq2:=v=cte;eqEq2:=dv/dz=0;eqEq3:=mu[i]+M[i]*g*z=cte;eqEq3:=dmu[i]/dz+M[i]*g=0;

>	eqEH:=0=0-V*dp-Sum(n[i]*M[i]*g*dz,i);eqEH:=0=-Vdp-n*M[m]*g*dz;eqEH:=0=-dp-rho*g*dz;

>	eqEHi:=dmu_dp[i]*dp_dz+dmu_dx[i]*dx_dz[i]+M[i]*g=0;

>	dmu_dp[i]:=dV_dn[i];dmu_dp[i]:=-V/n;dp_dz:=-n*M[m]/V*g;dmu_dx[i]:=R[u]*T/x[i];

>	eqEHi;dlnx[i]/dz=(M[m]-M[i])*g/(R[u]*T);

Pero eso vale igual para mezclas moleculares que para mezclas coloidales, cambiando las Ms por la masa de las partículas y la Ru por la k=Ru/NA:

a) Establecer la relación entre la variación de la concentración y las densidades.

>	dlnx[i]/dz=Vpart*(rho-rho2)*g/(k[B]*T);

b) Estimar el número de Avogadro.

>	N[Av]:=dlnc_dz/(Vpart*(rho-rho2)*g/(R[u]*T));

>	Vpart:=Pi*Di^3/6;Vpart_:=evalf(subs(dat,Vpart));N[A_]:=evalf(subs(Const,dlnc_dz=ln(1/2)/Dz12,dat1,N[Av]));

>	dlnN_N:=-dlnDz/Dz+dlnT/T-3*dlnDi/Di_-dlnrho/rho;SNN:=sqrt(STT^2+(3*SDD)^2+Srhorho^2+Szz^2);'SNNterms'=Sqrt(evalf(subs(dat,[STT^2,(3*SDD)^2,Srhorho^2,Szz^2]),3));SNN_:=subs(dat1,SNN):'SNN'=evalf(%,2);

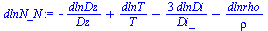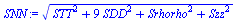lo que más influye es la incertidumbre en el tamaño; la SDD.

>	Nmin_:=N[A_]*(1-SNN_):'Nmin'=evalf(%,2);Nmax_:=N[A_]*(1+SNN_):'Nmax'=evalf(%,2);Nexact_:=subs(Const,N[A]);

Queda ligeramente fuera del intervalo de incertidumbre estándar; no es raro, pero indica que las incertidumbres de partida eran algo optimistas.

>