| > | restart;#"m07_p10" |
Se ha medido el contenido de una botella de 25 litros de butano comercial, resultando ser 10 kg, así como su presión a la temperatura ambiente de 15 °C, resultando ser 250 kPa. Se pide:
a) Suponiendo que el contenido es n butano puro, calcular la presión que debería haberse obtenido en la medida.
b) En ese caso, calcular el volumen de líquido y la fracción másica de vapor.
c) En ese caso, supóngase que se desea calentar el contenido hasta 45 °C, e indíquese cómo se calcularíael calor necesario, dando una estimación de su valor.
d) En el caso de que, a temperatura ambiente, al abrir la válvula saliese un gasto de 6 litros por minuto medido a 15 °C y 100 kPa, calcular el gasto másico y el flujo de calor recibido del exterior para mantener constante la temperatura.
e) Suponiendo en lo sucesivo que el butano comercial es una mezcla de n butano y propano, determinar las curvas de burbuja y de rocío de las posibles mezclas a temperatura ambiente en el diagrama p x (presión composición).
f) Calcular las fracciones molares en cada fase.
g) Indicar cómo iría variando la composición con el tiempo al dejar salir gas de la botella.
h) Calcular el coste energético mínimo para la separación de los componentes que salen, a presión y temperatura atmosféricas.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su1:="C4H10":su2:="C3H8":dat:=[V=0.025*m_^3,m=10*kg_,T1=288*K_,p1=250e3*Pa_,T2=(45+273)*K_,Vdot=6e-3/60*m_^3/s_]; |

Eqs. const.: 1=butano, 2=propano.
| > | eqETg:=subs(eq1_11,eq1_12);eqEE:=eq1_16;g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end: |
a) Suponiendo que el contenido es n butano puro, calcular la presión que debería haberse obtenido en la medida.
| > | p1but_:=evalf(subs(dat,pv1(T1)));p1but_Cla:=subs(dat1,evalf(subs(dat1,dat,p0*exp(-(h[lv0]/R)*(1/T1-1/T[b]))))); |
i.e. a 15 ºC, con la ecuación de Antoine debería estar a 175,8 kPa (con la ecuación de Clausius-Clapeyron a 164,2 kPa; con los datos del NIST a 176,2 kPa). Se concluye que no puede ser n-butano puro si a 15 ºC tiene una presión de 250 kPa.
b) En ese caso, calcular el volumen de líquido y la fracción másica de vapor.
Podemos suponer que casi toda la masa va a estar líquida (se comprueba después). Usaremos la densidad que viene en la Tabla.
| > | rho1but:=subs(dat1,rho);Vl_:=subs(dat1,m/rho);mw:=p1[but]*(V-Vl)/(R[B]*T1);mv_:=subs(dat1,p1but_*(V-Vl_)/(R*T1));x1_:=subs(dat1,mv_/m); |
i.e. con el modelo de líquido perfecto (rho=cte=602 kg/m3), de los 25 L habría 16,6 L en estado líquido y 8,4 L en estado gaseoso (36 g), y la fracción másica de vapor sería del 0,36 % (con los datos del NIST, a 15 ºC es rhoL=584 kg/m3, rhoV=4,55 kg/m3, habría 17,2 L de líquido y sería x=0,36 %).
c) En ese caso, supóngase que se desea calentar el contenido hasta 45 °C, e indíquese cómo se calcularía el calor necesario, dando una estimación de su valor.
| > | Q:=DU;Q:=DH-DpV;Qaprox:=m*c*(T2-T1);Qaprox_:=subs(dat1,Qaprox);p2_:=evalf(subs(dat,pv1(T2)));eqv:=V/m=(1-x)/rho+x*R*T2/p2;x2_:=subs(p2=p2_,dat1,solve(eqv,x));h=(1-x)*hl+x*hv;hl=hl(T);hv=hv(T);h1l_:=subs(dat1,T=T1,dat1,hl(T));h1v_:=subs(dat1,T=T1,dat1,hv(T));h1_:=(1-x1_)*h1l_+x1_*h1v_;h2l_:=subs(dat1,T=T2,dat1,hl(T));h2v_:=subs(dat1,T=T2,dat1,hv(T));h2_:=(1-x2_)*h2l_+x2_*h2v_;Q_:=subs(dat1,m*(h2_-h1_)-(p2_-p1)*V); |
i.e. en primera aproximación, Q=mcDT=720 kJ, y teniendo en cuenta el cambio de fase Q=730 kJ (con datos NIST, Q=m(u2-u1)=10·(311-236)=748 kJ).
d) En el caso de que, a temperatura ambiente, al abrir la válvula saliese un gasto de 6 litros por minuto medido a 15 °C y 100 kPa, calcular el gasto másico y el flujo de calor recibido del exterior para mantener constante la temperatura.
| > | mdot:=rho*Vdot;rho0_:=subs(dat1,p0/(R*T0)):'rho0'=evalf(%,3);mdot_:=subs(rho=rho0_,dat1,mdot);Qdot:='mdot'*hlv*(1+vl/vv);Qdot_:=subs(dat1,mdot_*h[lv0]); |
i.e. salen 0,2 g/s de gas, y deben entrar 88 W desde el exterior para mantener la vaporización.
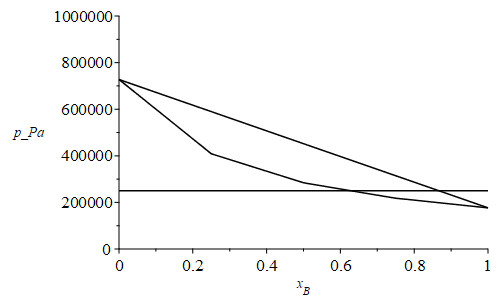
e) Suponiendo en lo sucesivo que el butano comercial es una mezcla de n-butano y propano, determinar las curvas de burbuja y de rocío de las posibles mezclas a temperatura ambiente en el diagrama p-x (presión-composición).
| > | eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p; |
| > | sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});sol1_250:=evalf(subs(p=p1,pv1=pv1(T1),pv2=pv2(T1),dat,sol1));assign(sol1): |
i.e. a 15 ºC y 250 kPa el líquido sería 86 % butano y 14 % propano, mientras que el gas sería 61 % butano y 39 % propano. Para dibujar el diagrama p-x podríamos dar valores intermedios de la composición del vapor saturado:
| > | p1_:=evalf(subs(Const,pv1(T0)));p2_:=evalf(subs(Const,pv2(T0)));p[boil025_]:=solve(0.25=subs(pv1=p1_,pv2=p2_,xv1),p);p[dew025_]:=solve(0.25=subs(pv1=p1_,pv2=p2_,xl1),p);p[boil05_]:=solve(0.5=subs(pv1=p1_,pv2=p2_,xv1),p);p[dew05_]:=solve(0.5=subs(pv1=p1_,pv2=p2_,xl1),p);p[boil075_]:=solve(0.75=subs(pv1=p1_,pv2=p2_,xv1),p);p[dew075_]:=solve(0.75=subs(pv1=p1_,pv2=p2_,xl1),p);plot(subs(dat,SI0,{[[0,p2_],[0.25,p[boil025_]],[0.5,p[boil05_]],[0.75,p[boil075_]],[1,p1_]],[[0,p2_],[0.25,p[dew025_]],[0.5,p[dew05_]],[0.75,p[dew075_]],[1,p1_]],[[0,p1],[1,p1]]}),'x[B]'=0..1,p_Pa=0..1e6,color=black); |
 |
f) Calcular las fracciones molares en cada fase.
Para 15 ºC y 250 kPa, se tendría:
| > | x_=subs(p=p1,pv1=p1_,pv2=p2_,dat,[''xv1''=xv1,''xv2''=xv2,''xl1''=xl1,''xl2''=xl2]);eqL:=ML/rhoL='xl1*M1/rhol1+xl2*M2/rhol2';ML:='xl1*M1+xl2*M2';ML_:=subs(p=p1,pv1=p1_,pv2=p2_,dat,M1=M,dat1,M2=M,dat2,ML);rhoL_:=subs(p=p1,pv1=p1_,pv2=p2_,dat,M1=M,rhol1=rho,dat1,M2=M,rhol2=rho,dat2,ML_/rhs(eqL));VL:=mL/rhoL;VL_:=subs(dat,m/rhoL_); |
i.e. en fase líquida habría 87% de butano y 13 % de propano, con una densidad de 600 kg/m3, que ocuparían 16,7 litros. Con los datos del NIST sería xv1=0,68, xv2=0,32, xl1=0,89, xl2=0,11, rhoL=576 kg/m3, rhoV=5,90 kg/m3, xv0=0,0046 y Vl=17,3 litros.
g) Indicar cómo iría variando la composición con el tiempo al dejar salir gas de la botella.
Como sale más proporción de propano (el más volátil), cada vez queda proporcionalmente más butano dentroy por tanto la presión de equilibrio irá bajando hasta el límite p1_=p1 (desde 250 kPa hasta 176 kPa). Este descenso de presión es el que hace que cada vez salga el gas 'con menos fuerza', y no porque cada vez quede menos gas (si fuese butano puro y la transmisión de calor es suficiente, el gasto de salida no variaría con la masa interior). Nótese que, como al principio sale más proporción de propano, el gas que sale va teniendo cada vez más densidad, pero la disminución de presión es preponderante. Una botella de butano comercial a 15 ºC puede suministrar unos 0,9 kg/h al principio y unos 0,8 kg/h tras una hora de funcionamiento.
h) Calcular el coste energético mínimo para la separación de los componentes que salen, a presión y temperatura atmosféricas.
| > | wmin:='-R[u]*T0*(xv1*ln(xv1)+xv2*ln(xv2))';wmin_:=evalf(subs(Const,p=p1,pv1=p1_,pv2=p2_,dat,wmin));MV:='xv1*M1+xv2*M2';MV_:=subs(p=p1,pv1=p1_,pv2=p2_,dat,M1=M,dat1,M2=M,dat2,MV); |
i.e. costaría como mínimo 1,6 kJ/mol o 1,6/0,053=30 kJ/kg (unos 9 W para ir separando lo que va saliendo si salen 0,9 kg/h).
| > |