>	restart;#"m07_p09"

En un dispositivo cilindro émbolo hay 2 gramos de propano mezclados con 3 gramos de butano. Se pide:

a)•Fracciones molares.

b)•Presiones de evaporación y condensación a temperatura ambiente.

c)•Temperaturas de evaporación y condensación a 500 kPa.

d)•Fracciones molares a 500 kPa y 300 K, y volumen ocupado.

e)•Coste energético mínimo de separación de la mezcla en condiciones ambientes.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="C3H8":su2:="C4H10":dat:=[m1=0.002*kg_,m2=0.003*kg_,p1=500e3*Pa_,T1=300*K_,T0=(15+273.15)*K_];

Eqs. const.:

>

eqETg:=subs(eq1_11,eq1_12);eqEE:=eq1_16;g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});assign(sol1):

a)•Fracciones molares.

Suponemos n-butano.

>

y1:=m1/(m1+m2);y2:=m2/(m1+m2);x1:='(y1/M1)/(y1/M1+y2/M2)';x2:='(y2/M2)/(y1/M1+y2/M2)';rho0:='(p0/(R[u]*T0))*(x1*M1+x2*M2)';val_:=subs(Const,dat,M1=M,dat1,M2=M,dat2,[''y1''=y1,''y2''=y2,''x1''=x1,''x2''=x2,''rho0''=rho0]):evalf(%,3);x1_:=rhs(val_[3]):'x1'=evalf(%,3);x2_:=rhs(val_[4]):'x2'=evalf(%,3);

i.e. la densidad del gas a 15 ºC y 100 kPa es 2,15 kg/m3, y su 40% en masa de propano equivale al 47% molar.

b)•Presiones de evaporación y condensación a temperatura ambiente.

>

pv1_:=evalf(subs(Const,pv1(T0))):'pv1'=evalf(%,3);pv2_:=evalf(subs(Const,pv2(T0))):'pv2'=evalf(%,3);p[dew_]:=solve(x1_=subs(pv1=pv1_,pv2=pv2_,xv1),p):'p[dew]'=evalf(%,3);p[boil_]:=solve(x1_=subs(pv1=pv1_,pv2=pv2_,xl1),p):'p[boil]'=evalf(%,3);plot({[[0,pv2_/Pa_],[x1_,p[boil_]/Pa_],[1,pv1_/Pa_]],[[0,pv2_/Pa_],[x1_,p[dew_]/Pa_],[1,pv1_/Pa_]]},x=0..1,'p'=00..1e6,color=black);

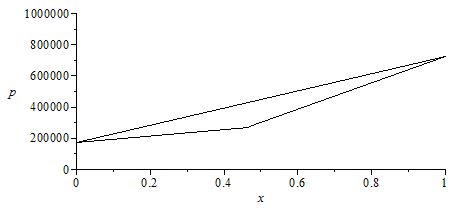i.e., a 15 ºC la pv(P)=725 kPa y la pv(B)=176 kPa. La mezcla de xP=47% empezaría a condensar a 272 kPa y acabaría de hacerlo a 432 kPa.

Nótese que se han unido con líneas reactas en el gráfico los puntos hallados (para x1=0,47); realmente la inferior es una curva suave.

c)•Temperaturas de evaporación y condensación a 500 kPa.

>

p1_:=subs(dat,p1);T1_:=solve(p1_=pv1(T),T);T2_:=solve(p1_=pv2(T),T);T[dew_]:=fsolve(x1_=subs(p=p1_,pv1=pv1(T),pv2=pv2(T),SI0,xv1),T=100..500)*K_;'T[dew_]'=TKC(%);T[boil_]:=fsolve(x1_=subs(p=p1_,pv1=pv1(T),pv2=pv2(T),SI0,xl1),T=100..500)*K_;'T[boil_]'=TKC(%);plot({[[0,T2_/K_],[x1_,T[dew_]/K_],[1,T1_/K_]],[[0,T2_/K_],[x1_,T[boil_]/K_],[1,T1_/K_]],[[0,300],[1,300]]},x=0..1,'T'=250..350,color=black);

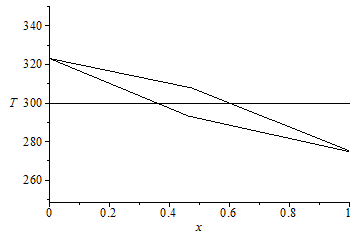i.e. a 500 kPa, la mezcla de xP=47% empezaría a hervir a 20 ºC y acabaría a 35 ºC.

Nótese que se han unido con líneas reactas en el gráfico los puntos hallados (para x1=0,47); realmente son curvas.

d)•Fracciones molares a 500 kPa y 300 K, y volumen ocupado.

>

T1_:=300*K_;xv1_:=evalf(subs(p=p1_,pv1=pv1(T1_),pv2=pv2(T1_),xv1));xl1_:=evalf(subs(p=p1_,pv1=pv1(T1_),pv2=pv2(T1_),xl1));xv2_:=1-xv1_:'xv2'=evalf(%,3);xl2_:=1-xl1_;V:='Vliq+Vvap';xl0_:=evalf(subs(sol2,x01=x1_,x02=x2_,p=p1_,pv1=pv1(T1_),pv2=pv2(T1_),xl0));xv0_:=evalf(subs(sol2,x01=x1_,x02=x2_,p=p1_,pv1=pv1(T1_),pv2=pv2(T1_),xv0));n:=m1/M1+m2/M2;n_:=subs(dat,M1=M,dat1,M2=M,dat2,n);nv:='n*xv0';nv_:=n_*xv0_;Mv:='xv1*M1+xv2*M2';Mv_:=subs(M1=M,dat1,M2=M,dat2,xv1_*M1+xv2_*M2);Vv:='nv*R[u]*T1/p1';Vv_:=subs(Const,dat1,dat,nv_*R[u]*T1/p1);'Vv_*1e6'=%*1e6;mv:='p1*Vv*Mv/(R[u]*T1)';mv_:=subs(dat,Const,dat1,p1*Vv_*Mv_/(R[u]*T1));'mv_*1e6'=%*1e6;ml:='m1+m2-mv';ml_:=subs(dat,m1+m2-mv_);Ml:='xl1*M1+xl2*M2';Ml_:=subs(M1=M,dat1,M2=M,dat2,xl1_*M1+xl2_*M2);eqv:='Ml/rhol=xl1*M1/rho1+xl2*M2/rho2';rhol_:=subs(M1=M,rho1=rho,dat1,M2=M,rho2=rho,dat2,Ml_/(xl1_*M1/rho1+xl2_*M2/rho2));Vl:='ml/rhol';Vl_:=ml_/rhol_;'Vl_'*1e6=%*1e6;

i.e. a 300 K y 500 kPa los 5 g de mazcla (2 de P y 3 de B), se distribullen en 3 g en fase líquida ocupando 5,2 cm3, más 2 g en fase gaseosa ocupando Vv=207 cm3 (212 cm3 en total).

e)•Coste energético mínimo de separación de la mezcla en condiciones ambientes.

>	Phi:='n*R[u]*T0*(x1_*ln(1/x1_)+x2_*ln(1/x2_))';Phi_:=subs(n=n_,Const,dat1,Phi);

i.e. costaría 161 J separar totalmente la mezcla en condiciones ambiente (en realidad, lo que se quiere decir es que costaría 1,7 kJ separar cada mol de mezcla gaseosa para obtener 0,47 moles de propano más 0,53 moles de butano, en condiciones estacionarias).

>