>	restart;#"m07_p08"

La composición de una partida de gas natural argelino se puede aproximar por xmetano=0,9 y xetano=0,1. Se pide:

a)•Fracciones másicas y densidad en condiciones ambientes.

b)•Límites de temperatura en que las mezclas metano etano pueden presentarse en estado bifásico a presión atmosférica.

c)•Para dos temperaturas intermedias entre las anteriores, determínese las composiciones de saturación, indicando los puntos correspondientes en un diagrama T x.

d)•Coste energético mínimo para la separación de los componentes.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CH4":su2:="C2H6":dat:=[x01=0.9,x02=0.1];

Eqs. const.:

>

eqETg:=subs(eq1_11,eq1_12);eqEE:=eq1_16;g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1_/p;eqE2:=xv2/xl2=pv2_/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});

a)•Fracciones másicas y densidad en condiciones ambientes.

>	y1:=x1*M1/(x1*M1+x2*M2);y2:=x2*M2/(x1*M1+x2*M2);rho0:=(p0/(R[u]*T0))*(x1*M1+x2*M2);val_:=subs(Const,M1=M,x1=x01,dat1,M2=M,x2=x02,dat2,[''y1''=y1,''y2''=y2,''rho0''=rho0]):evalf(%,3);

i.e. la densidad del gas es 0,73 kg/m3, y su 90% de CH4 molar equivale al 83% en masa.

b)•Límites de temperatura en que las mezclas metano etano pueden presentarse en estado bifásico a presión atmosférica.

Si no se tiene en cuenta la composición, serán las de ebullición de las sustancias puras (con el MMI).

>	T1_:=subs(dat1,evalf(subs(dat1,solve(p0=pv1(T),T))));T2_:=subs(dat2,evalf(subs(dat2,solve(p0=pv2(T),T))));

c)•Para dos temperaturas intermedias entre las anteriores, determínese las composiciones de saturación, indicando los puntos correspondientes en un diagrama T x.

Vamos a añadir otro valor de temperatura intermedia en cada intervalo, para que quede más suave la curva.

>

'xv1'=subs(sol1,xv1);'xl1'=subs(sol1,xl1);'xl0'=solve(subs(xv0=1-xl0,eqC1),xl0);N:=6:print(`T [K]  pv1 [kPa]    pv2 [kPa]  xv1   xl1  xl0`); pl1:=[[1,T1_/K_]]:pl2:=[[1,T1_/K_]]:for i from 1 to N-1 do T[i]:=(T1_+(T2_-T1_)*(i/N))/K_;pv1__:=evalf(pv1(T[i]*K_))/Pa_;pv2__:=evalf(pv2(T[i]*K_))/Pa_;xv1_[i]:=subs(sol1,p=p0/Pa_,Const,pv1_=pv1__,pv2_=pv2__,xv1);xl1_[i]:=subs(sol1,p=p0/Pa_,Const,pv1_=pv1__,pv2_=pv2__,xl1);pl1:=[op(pl1),[xv1_[i],T[i]]];pl2:=[op(pl2),[xl1_[i],T[i]]];xl0_:=solve(subs(xv0=1-xl0,xv1=xv1_[i],xl1=xl1_[i],dat,eqC1),xl0);print(T[i],pv1__,pv2__,xv1_[i],xl1_[i],xl0_);od:pl1:=[op(pl1),[0,T2_/K_]]:pl2:=[op(pl2),[0,T2_/K_]]:pl3:=seq([[0,op(2,op(i,pl1))],[1,op(2,op(i,pl1))]],i=1..N+1):plot({pl1,pl2,pl3,[[0.9,0],[0.9,200]],[[1,0],[1,200]]},x=0..1,'T'=0..200,color=black);

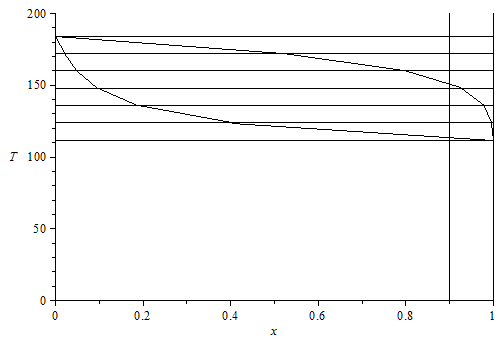Nótese que los valores negativos de la fracción molar de líquido, xl0, indican que sólo hay gas.

Si hubiéramos querido calcular los límites de temperatura para mezcla bifásica a composición global fija, se haría así:

>

eq1:=subs(xv1=x01,pv1_=pv1(T),p=p0,dat1,eqE1);eq2:=subs(xv2=1-x01,xl2=1-xl1,pv2_=pv2(T),p=p0,dat2,eqE2);fsolve(subs(SI0,{eq1,eq2}),{T,xl1},{T=100..200,xl1=0..1});Tcond_:=subs(%,T*K_);eq1:=subs(xl1=x01,pv1_=pv1(T),p=p0,dat1,eqE1);eq2:=subs(xv2=1-xv1,xl2=1-x01,pv2_=pv2(T),p=p0,dat2,eqE2);fsolve(subs(SI0,{eq1,eq2}),{T,xv1},{T=100..200,xv1=0..1});Tvap_:=subs(%,T*K_);

i.e., este gas empezaría a condensar a 151 K (con tan sólo un 8% de CH4 en las primeras gotas), y acabaría de condensar completamente a 113 K (con prácticamente un 100% de CH4 en las últimas burbujas).

d)•Coste energético mínimo para la separación de los componentes.

Para separar ambos componentes:

>	phi:=R[u]*T0*(x01*ln(1/x01)+x02*ln(1/x02));phi_:=evalf(subs(Const,dat,phi));

i.e. costaría 0,78 kJ separar cada mol de gas natural en 0,9 moles de metano más 0,1 moles de etano.

>