>	restart:#"m06_p68"

Se hace pasar dióxido de carbono líquido, proveniente de una botella que está a 17 ºC, a través de una válvula de expansión hasta casi la presión del punto triple (para evitar que se forme tapón de hielo seco), y posteriormente se vaporiza totalmente en un cambiador de calor. Se pide, resolver gráfica y analíticamente:
a) Presión y densidad del líquido a la entrada de la válvula.
b) Estado termodinámico a la salida de la válvula.
c) Calor necesario por unidad de gasto.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): su:="CO2":dat:=[T1=(17+273.15)*K_];

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),SI2,SI1:get_pv_data(su):

a) Presión y densidad del líquido a la entrada de la válvula.

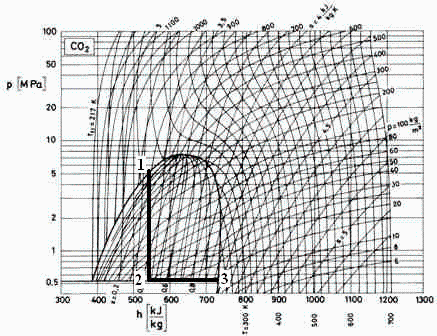
Suponemos disponible el diagrama de propiedades del CO2.

En la botella habrá líquido en equilibrio con algo de vapor, pero se extraerá sólo líquido (saturado), i.e. en el punto 1 del diagrama:, i.e. entre 5,0 MPa y 5,5 MPa y unos 800 kg/m3.

>	T1_:=subs(dat,T1);p1_dia:=5.3e6*Pa_;rho1_dia:=800*kg_/m_^3;

Si no dispusiéramos del diagrama, se podría usar el modelo de líquido ideal (MLI), rho=cte=823 kg/m3, o el modelo de estados correspondientes (MEC), rho=p/(ZRT) , con la p dada por la ecuación de Antoine, y la Z obtenida del diagrama Z-pR para pR=p/pcr y T=T/Tcr.

>	p1_Ant:=subs(dat,evalf(subs(dat,pv(T1))));pR1_:=subs(dat,p1_Ant/p[cr]);TR1_:=subs(dat,T1/T[cr]);Zliq:=0.11;rho1_MEC=subs(dat,p1_Ant/(Zliq*R*T1));

El resultado más preciso (datos del NIST) es: 5,311 MPa y rho=805,3 kg/m3.

b) Estado termodinámico a la salida de la válvula.

Suponiendo que la transmisión de calor en la válvula, y las energías cinéticas, son despreciables (frente a la energía térmica), el proceso será isoentálpico, y en el diagrama se ve que, bajando verticalmente desde el punto 1 (h1:=545*J_/kg_) hasta la linea triple (punto 2), se tiene p2=0,51 MPa y una fracción másica de vapor x2=0,42.

>	eqBE:=Dh=q+w;eqBE:=Dh=0;p2_dia:=510e3*Pa_;x2_dia:=0.42;

Si no dispusiéramos del diagrama, habría que usar la ecuación de Antoine para obtener p2 en el punto triple, que se aproxima por el de fusiín, Tf=217 K, y después determinar la x2 que anula h2-h1=(1-x2)*h2l+x2*h2v-h1=0; i.e. x=(h1-h2l)/(h2v-h2l).

Si usamos el modelo de sustancia perfecta:

>	T2_:=subs(dat,T[f]);p2_Ant:=subs(dat,evalf(subs(dat,pv(T2_))));eqBE:=(1-x2)*h2l+x2*h2v-h1=0;eqx:=x2=(h1-h2l)/(h2v-h2l);h1_h2l:=c[p]*(T1-T2);c_:=subs(dat,c);h1_h2l:=subs(dat,T2=T2_,dat,c*(T1-T2));h2v_h2l:=hlv[T2];h2v_h2l:=subs(dat,T=T2_,dat,hlv(T));eqx:=x=h1_h2l/h2v_h2l;

Si introducimos las correcciones por compresibilidad según el MEC, hay que resolver (1-x2)*Dh2lcc+x2*Dh2vcc-cp*(T1-T2)=0

>

eqBE:=-(1-x2)*Dh2lcc-x2*Dh2vcc-(cp*(T1-T2)-Dh1lcc)=0;cp_:=subs(dat,c[p]);pR1_:=subs(dat,p1_Ant/p[cr]);TR1_:=subs(dat,T1/T[cr]);Dh1lcc_:=37*J_/(mol_*K_);pR2_:=subs(dat,p2_Ant/p[cr]);TR2_:=subs(dat,T2_/T[cr]);Dh2lcc_:=51*J_/(mol_*K_);Dh2vcc_:=1.2*J_/(mol_*K_);x_:=subs(Dh2lcc=Dh2lcc_*T[cr]/M,Dh2vcc=Dh2vcc_*T[cr]/M,Dh1lcc=Dh1lcc_*T[cr]/M,cp=cp_,T2=T2_,dat,solve(eqBE,x2));

Nótese el diferente grado de aproximación: x=0,42 con el diagrama, x=0,73 con el MSP, x=0,46 con el MEC, y x=0,47.

>	Ttr:=216.58*K_;ptr:=518e3*Pa_;h1l:=45.75e3*J_/kg_;h2l:=-118.5e3*J_/kg_;h2v:=230.7e3*J_/kg_;x:=(h1l-h2l)/(h2v-h2l);eqBE_HE:=q='h2v-h1l';%;

c) Calor necesario por unidad de gasto.

Según el diagrama, h2v-h1l=unos 190 kJ/kg; según el MSP h2v-h1l=(h2v-h2l)-(h1l-h2l)=300-220=80 kJ/kg; según el MEC h2v-h1l=Dh1l-(Dh2v+x2*Dh2l)=150 kJ/kg; y según los datos del NIST h2v-h1l=184 kJ/kg.

>