>	restart:#"m06_p67"

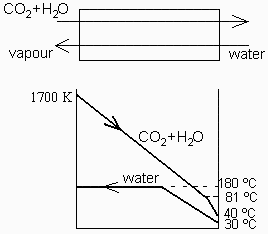
Se quiere aprovechar la energía de los gases de salida de un proceso de oxi-combustión, un flujo equimolar de CO2 y H2O a 1700 K y 0,2 MPa, para generar vapor saturado a 1 MPa a partir de agua a 30 ºC. Se pide:
a) Plantear el balance energético del recuperador de calor, indicando un valor representativo de la capacidad térmica de la mezcla gaseosa.
b) Determinar la temperatura mínima de salida de los gases, sabiendo que en el recuperador de calor debe haber un salto mínimo de 10 K.
c) Flujo de vapor generado relativo al de gases.

Datos:

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

>	su1:="CO2":su2:="H2O":dat:=[x1=0.5,T1=1700*K_,p2=1e6*Pa_,T0=(30+273)*K_,DT=10*K_];

Eqs. const.:

>	Cdat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:get_pv_data(su2):

a) Plantear el balance energético del recuperador de calor, indicando un valor representativo de la capacidad térmica de la mezcla gaseosa.

Supondremos el recuperador globalmente adiabático, i.e. el calor proviniente de los gases será el que pase al agua.

Habrá que ver si los gases se pueden enfriar por debajo de la temperatura del cambio de fase del vapor (pinch point).

Habrá que ver si se llega a condensar el vapor de los gases.

Se puede tomar un cp medio para la mezcla de gases de (47+54)/2=50 J/(mol·K), basándonos en los cp medios en procesos de combustión para el CO2 (54 J/(mol·K)) y para el H2O (47 J/(mol3K)), y en la relación equimolar en la mezcla (en base másica la ponderación sería distinta, claro). Al final haremos un estudio más preciso del cp medio, ya que la temperatura de 1700 K es algo baja para procesos de combustión.

>

eqBE:=mG*c[pGmass]*(T1-T2)=mW*(hv2-hl1);Tv=T[v](p2);Tv_:=evalf(subs(dat,solve(p2=pv(T),T)));hv2_:=subs(Wdat,T=Tv_,dat,hv(T));T1l:=T0+DT;T1l_:=subs(dat,%);hl1_:=subs(Wdat,T=T1l_,dat,hl(T));cp1_:=subs(cpComp,c[p,CO2]);cp2_:=op(2,op(6,[cpComp]));cp_mean:=(x1*cp1+x2*cp2);cp_mean_:=subs(x2=1-x1,dat,(x1*cp1_+x2*cp2_));cp_mean_m:=(x1*cp1+x2*cp2)/(x1*M1+x2*M2);cp_mean_m:=subs(x2=1-x1,cp1=cp1_,cp2=cp2_,M1=M,Cdat,M2=M,Wdat,dat,%);

i.e. el cp medio es de unos 50 J/(mol·K) o 1600 J/(kg·K).

b) Determinar la temperatura mínima de salida de los gases, sabiendo que en el recuperador de calor debe haber un salto mínimo de 10 K.

Si se supone que el salto mínimo ocurre en el extremo frío, los gases saldrían a 30+10=40 ºC, pero hay que comprobar que el acercamiento no llega a los 10 ºC.

>

T2:=T0+DT;T2_:=subs(dat,%);eqBE:='mG*c[pGmass]*(T1-T2)=mW*(hv2-hl1)';eqBE:=mV/mG='cp_mean_m*(T1-T2)/(hv2_-hl1_)';eqBE_:=subs(dat,%);eqBEvap:='mG*c[pGmass]*(T1-T2pinch)=mW*(hv2-hl2)';hl2_:=subs(Wdat,T=Tv_,dat,hl(T));eqBEvap_:=rhs(eqBE_)='cp_mean_m*(T1-T2pinch)/(hv2_-hl2_)';T2pinch_:=solve(subs(dat,%),T2pinch);eqCheck:=DTpinch='T2pinch_-Tv_';%;

Hay que ver si condensa al vapor.

>	eqDew:=subs(phi=1,eq8_4);TDew_:=evalf(subs(dat,solve((1-x1)*p0=pv(T),T)));xv_s:=p[v](T[s])/p0;xv_s_:=subs(dat,pv(T2_)/p0);

Efectivamente, la condensación de los gases empezaría a 354 K (81 ºC), y a los 40 ºC de salida ya habría condensado casi todo el vapor (un85%, desde xv=0.5 hasta xv=0.07).

c) Flujo de vapor generado relativo al de gases.

Contando con la entalpía de condensación:

>	eqBE:='mG*(c[pGmass]*(T1-T2)+y2*hlv)=mW*(hv2-hl1)';y2:=x2*M2/(x1*M1+x2*M2);y2_:=subs(x2=1-x1,M1=M,Cdat,M2=M,Wdat,dat,%);hlv_:=subs(Wdat,T=T2_,dat,hlv(T));eqBE:=mV/mG='(cp_mean_m*(T1-T2)+y2_*hlv_)/(hv2_-hl1_)';eqBE_:=subs(dat,%);

i.e., se puede generar hasta 1,1 kg de vapor por cada kg de gases.

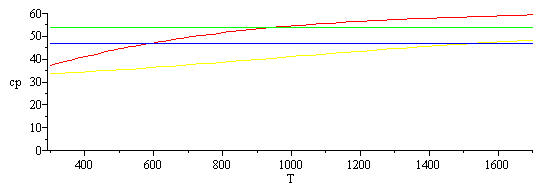
Si hacemos un cálculo más preciso del cp medio en el intervalo 452..1700 K, obtenemos 54 y 42 (en vez de 54 y 47).

>	cp1:=get_cp_data(su1);cp2:=get_cp_data(su2);plot(subs(SI0,[cp1,cp1_,cp2,cp2_]),T=300..1700,cp=0..60);cp1m_:=int(subs(SI0,cp1),T=452..1700)/(1700-452);cp2m_:=int(subs(SI0,cp2),T=452..1700)/(1700-452);

>