>	restart;#"m06_p65"

En un recipiente de 0,5 litros de capacidad, se quiere instalar un calentador eléctrico para poder generar un chorro de vapor a 1 MPa. Suponiendo despreciables las pérdidas de calor al exterior, se pide:
a) Potencia eléctrica mínima para que empiece a salir vapor a 1 MPa en menos de 10 minutos.
b) Tiempo máximo que podría estar generando vapor con esa potencia.
c) Energía mínima necesaria (límite termodinámico) para pasar el agua ambiente a vapor a 1 MPa, y comparación con la suministrada por la resistencia.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":dat:=[V=0.5e-3*m_^3,p1=1e6*Pa_,t01=10*60*s_];

Estados:=[0,1,2]:

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Potencia eléctrica mínima para que empiece a salir vapor a 1 MPa en menos de 10 minutos.

No se especifican las condiciones iniciales, así que supondremos que lo llenamos de agua ambiente.

Al echar el agua, es de suponer que estará en condiciones del ambiente, 15 ºC y 100 kPa, por lo que, al conectar la resistencia, la energía se va usando en calentar el agua a 100 kPa (una vez calentada la resistencia), ir expulsando el aire remanente del llenado (hasta que se cierra la válvula de desaireación), ir generando vapor a volumen constante hasta que se alcanza la presión de suministro, y luego ir generando vapor a presión constante mientras dure, todo ello unido a las pérdidas térmicas a través de las paredes (más el escape de aire húmedo caliente durante la desaireación).

Suponemos que se echa 0,5 litros de agua (y que queda un pequeño volumen adicional con aire).

>	P:=m*(h1-h0)/t01;eqMLP:=m=V*rho;eqMLP:=subs(dat,%);h0=h[L,T0,p0];h0_:=subs(dat,T=T0,dat,hl(T));h1=h[V,T1,p1];p[v]=p[u]*exp(A-B/((T/T[u]+C)));T1_:=subs(dat,evalf(subs(dat,solve(p1=pv(T),T))));T1=TKC(T1_);h1=h[L,T1,p1];h1_:=subs(dat,T=T1_,dat,hl(T));P_:=subs(eqMLP,h1=h1_,h0=h0_,dat,P);

i.e., se necesita como mínimo 570 W. Se supone que el volumen que ocuparía esta resistencia se contabilizaría aparte.

Las pérdidas por las paredes pueden estimarse suponiendo h=10 W/(m2.K) y un área externa apropiada a una temperatura apropiada, entre los 179 ºC si no se aislase y unos 5 ºC para que no queme al tocarla (luego se calcularía el espesor de aislante necesario).

>	eqA:=A=6*V^(2/3);eqA_:=subs(dat,%);Qdot:=h*A*(Twall-Tair);Qdot_45:=subs(h=10*W_/(m_^2*K_),eqA,Twall=(45+273)*K_,Tair=T0,dat,SI0,Qdot)*W_;Qdot_179:=subs(h=10*W_/(m_^2*K_),eqA,Twall=T1_,Tair=T0,dat,SI0,Qdot)*W_;

efectivamente, las pérdidas serían pequeñas incluso si no se aislase el recipiente.

b) Tiempo máximo que podría estar generando vapor con esa potencia.

>	t12=m/mdot;eqBE:='P'=mdot*hlv;mdot:='P'/hlv;'hlv'=h[lv,T1];hlv_:=subs(dat,T=T1_,dat,hlv(T));mdot_:=subs(dat,P_/hlv_);t12_:=subs(eqMLP,m/mdot_);

i.e., se podría estar generando 0,28 g/s de vapor a 1 MPa y 179 ºC durante unos 1800 s (media hora).

c) Energía mínima necesaria (límite termodinámico) para pasar el agua ambiente a vapor a 1 MPa, y comparación con la suministrada por la resistencia.

El consumo mínimo será la diferencia de exergías de esa masa de agua.

>	Wmin:=DE+p0*DV-T0*DS;DE:=m*c*DT;DV:=0;DS:=m*c*ln(T1/T0);Wmin_:=subs(dat,evalf(subs(eqMLP,dat,m*c*(T1_-T0)-T0*m*c*ln(T1_/T0))));Wreal:='DE';Wreal_:=subs(dat,evalf(subs(eqMLP,dat,m*c*(T1_-T0))));eta[x]:=Wmin_/Wreal_;

i.e., el rendimiento exergético es sólo del 21%, pero la simplicidad lo hace útil.

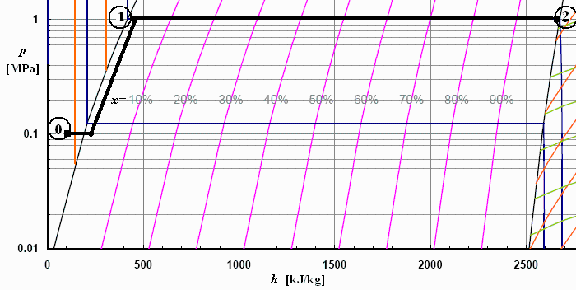
Se ha representado el proceso en un diagrama p-h a escala.

>