>	restart:#"m06_p64"

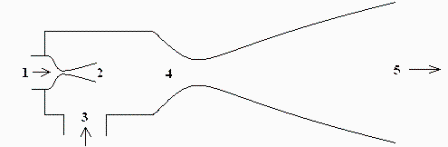
Considérese un eyector de vapor (Fig. 1) donde el fluido motriz entra saturado a 200 kPa (estado 1), se acelera en una tobera convergente-divergente que descarga a 10 kPa (estado 2), arrastra vapor saturado a esa presión (estado 3), y la mezcla (estado 4) se decelera en un difusor convergente-divergente hasta salir a presión atmosférica (estado 5). Sabiendo que entran 0,1 kg/s de vapor motriz, y que éste arrastra 0,01 kg/s de vapor aspirado, se pide:
a) Estudiar el proceso de 1 a 2, indicando los datos, las hipótesis, las ecuaciones relevantes y calculando la temperatura de salida en 2.
b) Estudiar el proceso de mezcla (2-34), indicando los datos, las hipótesis, las ecuaciones relevantes y calculando el estado en 4.
c) Estudiar el proceso de 4 a 5, indicando los datos, las hipótesis, las ecuaciones relevantes y calculando la temperatura de salida en 5.

d) Esquema de los procesos en el diagrama de Mollier.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(xL>0):

>	su:="H2O":dat:=[p1=200e3*Pa_,p2=10e3*Pa_,m1=0.1*kg_/s_,m3=0.01*kg_/s_];

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Estudiar el proceso de 1 a 2, indicando los datos, las hipótesis, las ecuaciones relevantes y calculando la temperatura de salida en 2.

Datos: p1,m1

Hipótesis: v1=0, Q12=0, Emdf12=0. Es una expansión isoentrópica en medio bifásico (no vale el MGP p*V^gamma=cte)

Ecuaciones: m2=m1, Dht=q+w queda h2+v2^2/2=h1, Ds=q/T+sgen=0, y el equilibrio bifásico T2(p2).

>	eqBM:=m2=m1;eqBE:=Dht=w+q;eqBS:=Ds=q/T+s[gen];s[gen]=0;q:=0;w:=0;ht=h+v^2/2;eqBE:=h2+v2^2/2=h1;eqClap:p=p[v](T);p1=subs(dat,p1);T1_:=subs(dat,evalf(subs(dat,solve(p1=pv(T),T)))):T1=evalf(%,3);T1=TKC(T1_);p2=subs(dat,p2);T2_:=subs(dat,evalf(subs(dat,solve(p2=pv(T),T)))):T2=evalf(%,3);T2=TKC(T2_);

Para luego necesitaremos las entalpías:

>

h1_:=subs(dat,T=T1_,dat,hv(T)):h1=evalf(%,3);s1_:=subs(dat,evalf(subs(dat,T=T1_,p=p1,dat,sv(T,p)))):s1=evalf(%,3);eqBS:=s2=s1;eqsx:=s2=(1-x2)*s2l+x2*s2v;s2v_:=subs(dat,evalf(subs(dat,T=T2_,p=p2,dat,sv(T,p)))):s2v=evalf(%,3);s2l_:=subs(dat,evalf(subs(dat,T=T2_,p=p2,dat,sl(T,p)))):s2l=evalf(%,3);x2_:=(s1_-s2l_)/(s2v_-s2l_):x2=evalf(%,2);eqhx:=h2=(1-x2)*h2l+x2*h2v;h2l_:=subs(dat,T=T2_,dat,hl(T)):h2l=evalf(%,3);h2v_:=subs(dat,T=T2_,dat,hv(T)):h2v=evalf(%,3);h2_:=(1-x2_)*h2l_+x2_*h2v_:'h2'=evalf(%,3);eqBE;v2_:=subs(dat,sqrt(2*(h1_-h2_))):v2=evalf(%,3);

i.e. el proceso de 1 a 2 es una conversión isoentrópica de energía de presión a energía cinética.

b) Estudiar el proceso de mezcla (2-34), indicando los datos, las hipótesis, las ecuaciones relevantes y calculando el estado en 4.

Datos: m2,m3,h2

Hipótesis: v3=0, Q=0, W=0. Es una simple mezcla isoentálpica a presión constante.

Ecuaciones: m4=m2+m3, Dht=q+w queda h2+v2^2/2+h3+v3^2/2=h4+v4^2/2, y el equilibrio bifásico T2(p2).

>

eqBM:=m2+m3=m4;m4_:=subs(dat,m1+m3);eqBE:=m2*ht2+m3*ht3=m4*ht4;eqBE:=m2*(h2+v2^2/2)+m3*(h3+v3^2/2)=m4*(h4+v4^2/2);eqBF:=m2*v2=m4*v4;v4_:=subs(dat,v2_*m1/(m1+m3)):v4=evalf(%,3);v3:=0;p3:=p2;T3:=T2;T3_:=T2_:h3_:=subs(dat,T=T3_,dat,hv(T)):h3=evalf(%,3);h4_:=subs(dat,(m1*(h2_+v2_^2/2)+m3*h3_)/m4_-v4_^2/2):h4=evalf(%,3);x4=(h4-h2l)/(h2v-h2l);x4_:=(h4_-h2l_)/(h2v_-h2l_):'x4'=evalf(%,2);s4_:=(1-x4_)*s2l_+x4_*s2v_:'s4'=evalf(%,3);

i.e. el vapor vivo a 950 m/s arrastra vapor muerto hasta quedar ambos a 870 m/s.

c) Estudiar el proceso de 4 a 5, indicando los datos, las hipótesis, las ecuaciones relevantes y calculando la temperatura de salida en 5.

Datos: m4,p4,T4,p5.

Hipótesis: v5=0, Q45=0, Emdf45=0. Es una compresión en medio bifásico, que no sería estrictamente isoentrópica porque las gotitas se calentarían mucho menos que el vapor, y se generaría entropí por mezcla con salto térmico, pero será pequeño el efecto y lo despreciaremos en este cálculo.

Ecuaciones: m4=m5, Dht=q+w queda h4+v4^2/2=h5+v5^2/2, Ds=0. Si sale bifásico será T5=Tv(p5).

Suponiendo x5<1:

>	eqBM:=m4=m5;eqBE:=h4+v4^2/2=h5+v5^2/2;eqBS:=s4=s5;p5:=p0;p5_:=subs(dat,p5);T5_:=subs(dat,evalf(subs(dat,solve(p5=pv(T),T)))):T5=evalf(%,3);T5=TKC(T5_);s5v_:=subs(dat,evalf(subs(dat,T=T5_,p=p5,dat,sv(T,p)))):s5v=evalf(%,3);s4=evalf(s4_,3);

luego, sí sale bifásico (s4<s5v), y por tanto:

>

s5l_:=subs(dat,evalf(subs(dat,T=T5_,p=p5,dat,sl(T,p)))):s5l=evalf(%,3);x5=(s5-s5l)/(s5v-s5l);x5_:=(s4_-s5l_)/(s5v_-s5l_):x5=evalf(%,4);h5v_:=subs(dat,T=T5_,dat,hv(T)):h5v=evalf(%,3);h5l_:=subs(dat,T=T5_,dat,hl(T)):h5l=evalf(%,3);h5=(1-x5)*h5l+x5*h5v;h5_:=(1-x5_)*h5l_+x5_*h5v_:h5=evalf(%,3);v5=sqrt(v4^2+2*(h4-h5));v5_:=subs(dat,sqrt(v4_^2+2*(h4_-h5_))):v5=evalf(%,3);

Un poco alta parece la velocidad de salida.

En la práctica, la tobera se suele diseñar con un cuello largo donde tiene lugar una deceleración brusca, así que el proceso aquí idealizado, y que se representa en la Fig. 1, puede que se parezca más en la práctica al de la Fig. 2.

>

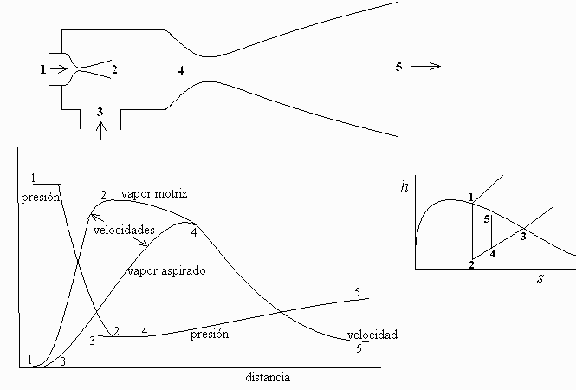
Fig. 1. Eyector con difusor adaptado.

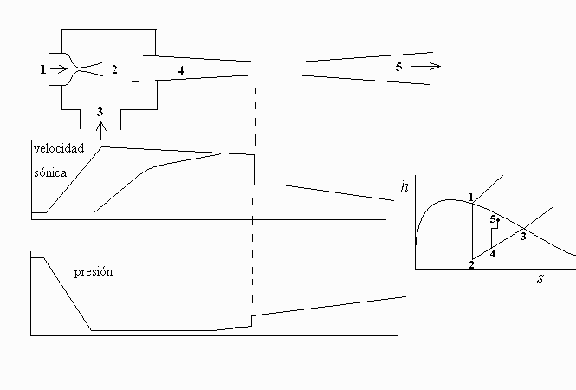
Fig. 2. Eyector con difusor de cuello largo.