>	restart;#"m06_p60"

Una planta regasificadora de gas natural licuado (LNG) ha de producir 100 kg/s de gas natural a 8 MPa para alimentar el gasoducto de salida, a partir del LNG a presión atmosférica de los tanques de almacenamiento del LNG traido por barco. Se pide:
a) ¿Se necesita aportar exergía en el proceso descrito, o por el contrario se podría con ello producir trabajo?
b) ¿Qué es mejor, primero comprimir y luego atemperar, o al revés? Estimar el coste mínimo de compresión del líquido y el de compresión del gas.
c) En la realidad, debido a la inevitable transmisión de calor a través de las paredes del tanque de LNG, existe una auto-regasificación (boil-off) de 1 kg/s, que, o bien se ha de quemar para minimizar el daño ecológico de su emisión, o se ha de volver a licuar (que resulta muy caro), o se comprime para el suministro a 8 MPa (que resulta muy caro), o se quema para acelerar la regasificación del resto (como así se hace en la práctica), o se aprovecha en la forma siguiente: el vapor autogenerado (el boil-off) es comprimido sólo hasta una presión intermedia pi tal que al mezclarlo con el LNG destinado a la regasificación (comprimido también hasta pi), quede todo en fase líquida, completando luego la compresión hasta los 8 MPa de suministro al gasoducto. Determinar la presión intermedia.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CH4":dat:=[m1=100*kg_/s_,p1=8e6*Pa_,m_boiloff=1*kg_/s_];

Esquema:

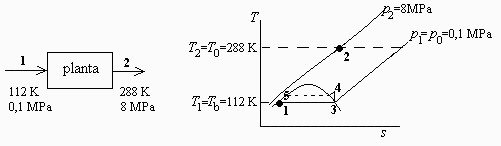
Fig 1. Esquema de entrada y salida de una planta de regasificación de LNG, y diagrama T-s correspondiente.

Eqs. const.:

>	gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):dat:=op(dat),Const,gdat,ldat,SI2,SI1:T_LNG:=subs(dat,T[b]);get_pv_data(su1):

a) ¿Se necesita aportar exergía en el proceso descrito, o por el contrario se podría con ello producir trabajo?

Como de costumbre, el gas natural se asimila a metano puro.

El balance exergético por unidad de gasto másico es:

>

eqBX:=psi[LNG]=psi[1]+w[u,out]-Int(1-T0/T,dQ)+T0*s[gen];psi:=dh-T0*ds;psi[LNG]:=-c[p]*(T0-T[b])-h[lv0]-T0*(-c[p]*ln(T0/T[b])-R*ln(p0/p0)-h[lv0]/T[b]);psi_LNG:=subs(dat,evalf(subs(dat,%))):'psi[LNG]'=evalf(%,3);psi[1]:=subs(T1=T0,c[p]*(T1-T0)-T0*(c[p]*ln(T1/T0)-R*ln(p1/p0)));psi1_:=subs(dat,evalf(subs(dat,%))):'psi[1]'=evalf(%,3);w[u,out,max]:='psi[LNG]-psi[1]';w_:=subs(dat,evalf(subs(dat,%))):'w[u,out,max]'=evalf(%,3);W[u,out,max]:=evalf(subs(dat,m1*w_),2);

donde sólo se ha contabilizado la exergía termomecánica, tomando como referencia el estado ambiente y usando modelos perfectos para el líquido y el gas.

Es decir, se podría con ello producir trabajo (en el límite, 43 MW). Una realización práctica podría ser mediante un motor témico del tipo de turbina de vapor, que usase un fluido de trabajo como el propano, que condensaría por contacto con el LNG, se bombearía el líquido hasta unos 500 kPa, se vaporizaría por contacto térmico con el ambiente, y produciría trabajo en su expansión en una turbina hasta unos 50 kPa, entrando en el condensador y cerrándose el ciclo.

Pese a que no es necesario aportar exergía, en el proceso se aporta mucha energía, pero del ambiente.

El balance energético es:

>	eqBE:=w+q=h[LNG]-h[1];eqBE:=w+q=h[lv0]+c[p]*(T0-T[b]);eqBE_:=subs(dat,%):evalf(%,2);

i.e., hay que aportarle 94 MW netos (suma algebraica de trabajos y calores) al fluido.

b) ¿Qué es mejor, primero comprimir y luego atemperar, o al revés? Estimar el coste mínimo de compresión del líquido y el de compresión del gas.

Siempre cuesta menos comprimir en frío, y especialmente cuesta mucho menos comprimir un líquido que su vapor.

Soponiendo, como de costumbre, proceso rápido y por tanto adiabático, en el límite isentrópico y con modelos de sustancias perfectas, será:

>	w[min]:=dh;w[min,liq]:=(p1-p0)/rho;wliq_:=subs(dat,%):'w[min,liq]'=evalf(%,2);w[min,gas]:=c[p]*(T2-T1);w[min,gas]:=c[p]*T0*((p1/p0)^((gamma-1)/gamma)-1);wgas_:=subs(dat,%):'w[min,gas]'=evalf(%,2);

i.e. pasar el líquido de 100 kPa y su T hasta 8 MPa y la T que corresponda (la misma con esas hipótesis), apenas cuesta 14 kJ/kg (1,4 MW los 100 kg/s), mientras que pasar el gas de 100 kPa y T0 hasta 8 MPa y la T que corresponda (bastante alta), costar\134134355a 1200 kJ/kg (120 MW los 100 kg/s). N\134363tese que, aunque no se comprima el gas sino el l\355quido, si se hiciera, se har\134355a en varias compresiones escalonadas con refrigeraci\134363n intermedia, para disminuir el consumo energ\134351tico.

Nótese que al aportar 1,4 MW de bombeo del líquido, los otros 93 MW del balance energ\351tico los aportar\355a el ambiente. En el caso de que se dejase atemperar primero y luego se llevase a cabo la compresi\363n isentr\363pica, el ambiente dar\355a 94 MW durante el atemperamiento, la compresi\363n del gas le dar\355a 120 MW m\341s, pero en el atemperamiento subsiguiente esos 120 MW pasar\355an al ambiente.

El haber usado modelos de sustancias perfectas no está mal para este análisis preliminar (las correcciones por compresibilidad no serán muy grandes); mucho más importante es el haber supuesto compresiones isentrópicas. Con datos del diagrama p-h del CH4, a 15 ºC y 100 kPa h=605 kJ/kg y s=11,55 kJ/(kg.K), y la compresión isentrópica hasta 8 MPa da T=660 K y h=1650 kJ/kg; i.e. wmin=Dh=1650-605=1045 kJ/kg en lugar de 1200 kJ/kg.

Si en lugar del límite adiabático se calcula el límite termodinámico máximo, será

>	w[min]:=dh-T0*ds;w[min,liq]:=(p1-p0)/rho;wliq_:=subs(dat,%):'w[min,liq]'=evalf(%,2);w[min,gas]:=c[p]*(T2-T1)-T0*(c[p]*ln(T2/T1)-R*ln(p2/p1));w[min,gas]:=T0*R*ln(p1/p0);wgas_:=subs(dat,evalf(subs(dat,%))):'w[min,gas]'=evalf(%,2);

i.e. en el límite termodinámico, se necesitarían 14 kJ/kg (1,4 MW para los 100 kg/s) para comprimir el l\355quido y 660 kJ/kg (66 MW para los 100 kg/s) para comprimir el gas.

c) En la realidad, debido a la inevitable transmisión de calor a través de las paredes del tanque de LNG, existe una auto-regasificación (boil-off) de 1 kg/s, que, o bien se ha de quemar para minimizar el daño ecológico de su emisión, o se ha de volver a licuar (que resulta muy caro), o se comprime para el suministro a 8 MPa (que resulta muy caro), o se quema para acelerar la regasificación del resto (como así se hace en la práctica), o se aprovecha en la forma siguiente: el vapor autogenerado (el boil-off) es comprimido sólo hasta una presión intermedia pi tal que al mezclarlo con el LNG destinado a la regasificación (comprimido también hasta pi), quede todo en fase líquida, completando luego la compresión hasta los 8 MPa de suministro al gasoducto. Determinar la presión intermedia.

La presión intermedia óptima es la mínima para que al mezclar 1 kg/s de vapor comprimido 'caliente', con los 99 kg/s necesarios de LNG comprimidos pero fríos, apenas se llegue a saturar el líquido, para que sea barato comprimirlo todo luego hasta los 8 MPa.

Seguimos con los modelos de sustancias perfectas y referencia en el estado líquido en ebullición:

>

eqBE:=m_boiloff*h_boiloff_comp+m_rest*h_LNG=m1*h1_liq;h_boiloff_comp:=h[lv0]+c[p]*(T_boiloff_comp-T[b]);T_boiloff_comp:=T[b]*(pint/p0)^((gamma-1)/gamma);m_rest:=m1-m_boiloff;h_LNG:=0;h1_liq:=c*(Tv_pint-T[b]);T_:=fsolve(subs(pint=pv(T),Tv_pint=T,dat,SI0,eqBE),T=0..1000)*K_:'Tv_pint'=evalf(%,4);pint_:=pv(T_):'pint'=evalf(%,3);T_:=subs(pint=pint_,dat,T_boiloff_comp):'T_boiloff_comp'=evalf(%,3);w_boiloff:='c[p]*(T_boiloff_comp-T[b])';w_:=subs(dat,c[p]*(T_-T[b])):'w_boiloff'=evalf(%,2);

Pues resulta que basta comprimir un poco, de 100 kPa hasta 118 kPa. La razón es que tan sólo hay que relicuar un 1% del gasto másico.

Con el diagrama p-h del CH4 habría que iterar para encontrar la solución. Supongamos que la pint=150 kPa (la primera dibujada).

A 0,1 MPa y 112 K, vapor saturado, h=225 kJ/kg y s=9,6 kJ/(kg.K), que comprimido isentrópicamente hasta 0,15 MPa da T=130 K y h=255 kJ/kg.

A 0,1 MPa y 112 K, líquido saturado, h=-290 kJ/kg y s=5 kJ/(kg.K), que comprimido isentr\363picamente hasta 0,15 MPa da T=112 K y h=-290 kJ/kg.

La entalpía de la mezcla será hmix=(mboiloff*hvapor+(m1-mboiloff)hliquido)=0,01*255+0.99*(-290)=-285 kJ/kg, que hay que compara con la entalpía de líquido saturado a 0,15 MPa (117 K) que es -270 kJ/kg, concluyéndose que la mezcla quedaría líquida sobrecomprimida, luego bastaría comprimir algo menos, como hasta los 0,118 MPa calculados.

Nótese que la regasificación es supercrítica, pues tine lugar a 8 MPa > pcr=4,6 MPa.

Puede compararse el coste de comprimir el boiloff de 10 kPa a 118 kPa, 10 kJ/kg (10 kW), que a unos 0,1 euros/kWh supondrían unos 1 euro/hora de consumo de electricidad, con el precio de tirarlo, que, a unos 0,5 euros/kg de precio de venta del GN, representaría una pérdida de 1800 euro/hora.

Se comprende que resultará muy conveniente instalar cerca de las plantas regasificadoras las nuevas centrales t\351rmicas de ciclo combinado, para ahorrar el transporte de gas, e industrias que consuman mucho frío (e.g. de congelación).

>

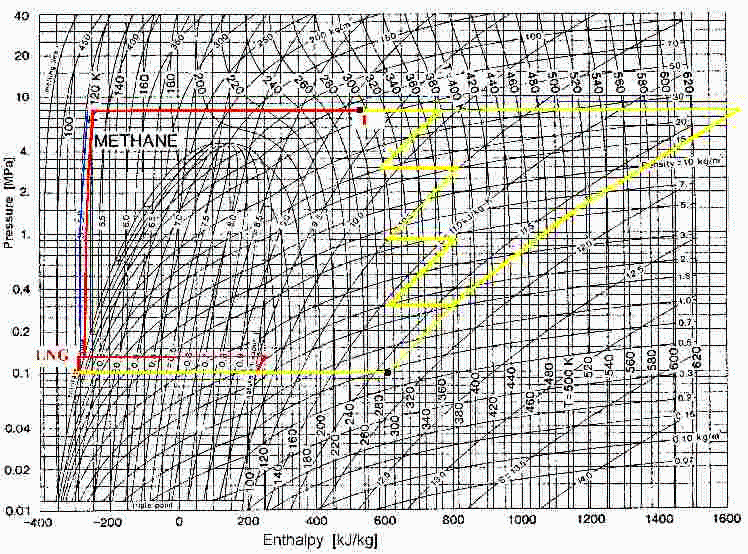
Fig. 2. Diagrama de las evoluciones contempladas en este problema: en rojo la buena y en amarillo la mala).