>	restart:#"m06_p59"

Se tiene un depósito rígido de 1 m3 conteniendo inicialmente vapor de agua a 200 kPa y 150 ºC. Se pide:
a) Estado final que alcanzaría si se dejase atemperar, haciendo un esquema del proceso en un diagrama T-s, y calculando los intercambios energéticos.
b) Trabajo máximo obtenible (límite termomecánico) en el estado inicial y en el final.
c) Plantear (incógnitas y ecuaciones) el estado final que se alcanzaría en el interior si se aislase térmicamente y se añadiese al vapor una masa igual de agua líquida a igual temperatura.
d) ¿Cómo se obtendría más trabajo en una turbina, haciendo una expansión hasta la presión atmosférica, o hasta la presión de vapor a temperatura atmosférica?. Ventajas e inconvenientes. Valores específicos iniciales.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="H2O":dat:=[V=1*m_^3,p1=200e3*Pa_,T1=(150+273)*K_];

Esquema:

>

>

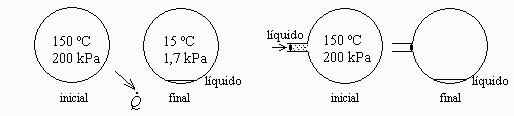
Ecs. const.:

>	gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):dat:=op(dat),Const,gdat,ldat,SI2,SI1:get_pv_data(su1):

a) Estado final que alcanzaría si se dejase atemperar, haciendo un esquema del proceso en un diagrama T-s, y calculando los intercambios energéticos.

>

pvT1_:=subs(dat,evalf(subs(dat,pv(T1)))):'p[v,T[1]]'=evalf(%,3);eqET:=rho=p1/(R*T1);eqET_:=rho=subs(dat,rhs(eqET)):evalf(%,3);m1:=rho[1]*V;m1_:=subs(dat,p1*V/(R*T1)):'m1'=evalf(%,3);T2:=T0;p2:=p[v,T[2]];p2_:=subs(dat,evalf(subs(dat,pv(T0)))):'p[v,T[2]]'=evalf(%,3);m2vap:='p2*V/(R*T2)';m2vap_:=subs(dat,p2_*V/(R*T2)):'m2vap'=evalf(%,2);x2:='mv2ap/m1';x2_:=m2vap_/m1_:'x2'=evalf(%,2);

i.e., inicialmente es todo vapor porque está sólo a 200 kPa y a esa T=150 ºC es pv=475 kPa.

Al atemperarse en un depósito rígido quedará bifásico a Tamb=15 ºC y su pv=1,7 kPa, condensando prácticamente toda la masa inicial (sólo quedan 13 g en fase vapor.

Balance energético (tomando como referencia el líquido en el punto triple):

>

eqBE:=DE=W+Q;H=U+pV;eqBE:=Q=DH-V*Dp;eqBE:='Q=m2vap*h2vap+m2liq*h2liq-m1*h1-V*(p2-p1)';h2vap_:=subs(dat,T=T2,dat,hv(T)):'h2vap'=evalf(%,2);h2liq_:=subs(dat,T=T2,dat,hl(T)):'h2liq'=evalf(%,2);h1_:=subs(dat,T=T1,dat,hv(T)):'h1'=evalf(%,2);m2liq_:='m1_-m2vap_';eqBE_:=subs(dat,Q=m2vap_*h2vap_+m2liq_*h2liq_-m1_*h1_-V*(p2_-p1)):evalf(%,2);

i.e. han salido 2,5 MJ por transmisión de calor al ambiente, como se podía haber previsto sin cálculo alguno pensando que era el calor de cambio de fase de 1 kg de agua a 15 ºC, unos 2,5 MJ.

b) Trabajo máximo obtenible (límite termomecánico) en el estado inicial y en el final.

Se trata de calcular la exergía necesaria para pasar 1,02 kg de agua ambiente al estado indicado.

Estado inicial:

>

DPhi:=DE+p0*DV-T0*DS;DPhi:=DH-D(pV)+p0*DV-T0*DS;DH:='m1*(h1-h0)';'h1'=evalf(h1_,2);h0_:=subs(dat,T=T0,dat,hl(T)):'h0'=evalf(%,2);DH_:=m1_*(h1_-h0_):'DH'=evalf(%,2);DpV:='(p1*V-p0*m1_/rho)';DpV_:=subs(dat,%):'DpV'=evalf(%,2);p0DV:='p0*(V-m1_/rho)';p0DV_:=subs(dat,%):'p0DV'=evalf(%,2);DS:='m1*(s1-s0)';s1_:=subs(dat,evalf(subs(dat,T=T1,p=p1,dat,sv(T,p)))):'s1'=evalf(%,2);s0_:=subs(dat,evalf(subs(dat,T=T0,dat,sl(T)))):'s0'=evalf(%,2);DPhi1_:=subs(dat,DH_-DpV_+p0DV_-T0*m1_*(s1_-s0_)):'Phi1'=evalf(%,2);

Estado final:

>

DPhi:=DE+p0*DV-T0*DS;DPhi:=DH-D(pV)+p0*DV-T0*DS;DH:='m2*(h2-h0)';m2_:=m1_:'h2'='(1-x2)*h2liq+x2*h2vap';h2_:=(1-x2_)*h2liq_+x2_*h2vap_:'h2'=evalf(%,2);h0_:=subs(dat,T=T0,dat,hl(T)):'h0'=evalf(%,2);DH_:=m2_*(h2_-h0_):'DH'=evalf(%,2);DpV:='(p2_*V-p0*m2_/rho)';DpV_:=subs(dat,%):'DpV'=evalf(%,2);p0DV:='p0*(V-m2_/rho)';p0DV_:=subs(dat,%):'p0DV'=evalf(%,2);DS:='m2*(s2-s0)';s2:='(1-x2)*s2liq+x2*s2vap';s2vap_:=subs(dat,evalf(subs(dat,T=T2,p=p2_,dat,sv(T,p)))):'s2vap'=evalf(%,2);s2liq_:=subs(dat,evalf(subs(dat,T=T2,dat,sl(T)))):'s2liq'=evalf(%,2);s2_:=(1-x2_)*s2liq_+x2_*s2vap_:'s2'=evalf(%,2);s0_:=subs(dat,evalf(subs(dat,T=T0,dat,sl(T)))):'s0'=evalf(%,2);DPhi2_:=subs(dat,DH_-DpV_+p0DV_-T0*m1_*(s2_-s0_)):'Phi2'=evalf(%,2);

i.e. inicialmente el trabajo máximo obtenible era de 590 kJ y tras el atemperamiento es de 98 kJ.

c) Plantear (incógnitas y ecuaciones) el estado final que se alcanzaría en el interior si se aislase térmicamente y se añadiese al vapor una masa igual de agua líquida a igual temperatura.

Sea el sistema completo depósito más cilindro-émbolo (i.e. toda el agua como sistema cerrado).

Si elegimos como incógnitas x3 y T3. Las ecuaciones serán la del balance másico (distribución interior) y la del balance energético.

>	eqBM:=m3='m1+m1';eqBMx:='V/m3=(1-x3)/rho+x3*R*T3/pv(T3)';eqBE:=DE=W+Q;Q:=0;W:=Int(p,DVliq);W:=0;eqBE:=DE=0;DH:='DH':eqBE:=DH-V*Dp=0;eqBE_m3:='(1-x3)*h3liq+x3*h3vap-(h1+h1liq)/2-(V/m3)*(p3(T)-p1)=0';x3:='(V/m3-1/rho)*pv(T3)/(R*T3)';

La resolución numérica es:

>

m3:=2*m1_:h1liq:=subs(dat,T=T1,hl(T)):h3liq:=subs(dat,hl(T)):h3vap:=subs(dat,hv(T)):eqBE_m3_:=subs(T3=T,dat,SI0,(1-x3)*h3liq+x3*h3vap-(h1_+h1liq)/2-(V/m3)*(pv(T3)-p1)=0):T3_:=solve(%,T)*K_:'T3'=evalf(%,3);x3_:=subs(dat,(V/m3-1/rho)*pv(T3_)/(R*T3_)):'x3'=evalf(%,2);p3_:=subs(dat,evalf(subs(dat,pv(T3_)))):'p3'=evalf(%,3);

i.e., al añadir adiabáticamente 1 kg de agua líquida a 150 ºC a un depósito con 1 kg de vapor a 150 ºC y 200 kPa, quedan los 2 kg en el depósito en estado bifásico a 121 ºC y 202 kPa (con una fracción másica de vapor del 54%).

Este apartado también se podría haber resuelto tomando como sistema el volumen de control del depósito, en cuyo caso el balance enerético sería DU=Q+W+hw*Dm, i.e. DH-D(pV)=cw*(T1-Tref)*m1, y con las aproximaciones anteriores DH-VDp=0, como antes.

>