>	restart:#"m06_p57"

Supóngase que el líquido dentro de un recargador de encendedores de gas es propano puro y está a 20 ºC. Se pide:
a) Presión interior (a la temperatura ambiente, y a 60 ºC que podría alcanzar al sol y resguardado).
b) Esquema en un diagrama T-s del proceso de salida, determinando la temperatura a la salida y la fracción másica de vapor..
c) Estimar cuánto podría enfriarse un dedal de latón de 10 g, al echar dentro de él 1 cm3 de propano líquido.
d) Índicar procedimientos que permitan determinar si el contenido es propano o butano.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="C3H8":su2:="Laton":dat:=[T0=(20+273)*K_,T60=(60+273)*K_,mS=0.010*kg_,V=1e-6*m_^3];

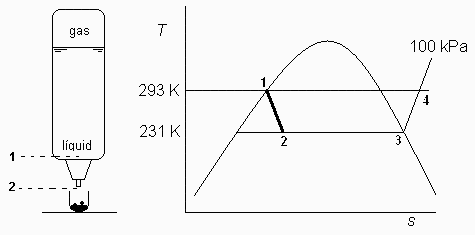
Esquema:

>

>

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):Sdat:=get_sol_data(su2):

a) Presión interior ( a la temperatura ambiente, y a 60 ºC que podría alcanzar al sol y resguardado).

>	p=p[v](T);pv20:=subs(dat,evalf(subs(dat,pv(T0)))):'pv20'=evalf(%,2);pv60:=subs(dat,evalf(subs(dat,pv(T60)))):'pv60'=evalf(%,2);;

b) Esquema en un diagrama T-s del proceso de salida, determinando la temperatura a la salida y la fracción másica de vapor..

El proceso de expansión en la válvula será isoentálpico. Ver esquema arriba. La Tsal será la de ebullición (bifásica a 100 kPa).

Tomamos hRef=0 para el líquido en el PT, y modelos de gas y de líquido perfectos.

>	T2=Tv(p0);T2_:=evalf(subs(dat,solve(p0=pv(T),T))):'T2'=evalf(%,3);h1:=c*(T1-TR);T1:=T0;TR:=T[f];h1_:=subs(dat,T=T1,dat,hl(T)):'h1'=evalf(%,2);h2:='c*(T2-TR)+x2*h[lv2]';h[lv2]:=subs(dat,T=T2_,dat,hlv(T)):'h[lv2]'=evalf(%,2);eq12:='h1=h2';x2_:=subs(T2=T2_,dat,solve(h1_=h2,x2)):'x2'=evalf(%,2);

c) Estimar cuánto podría enfriarse un dedal de latón de 5 g, al echar dentro de él 1 g de propano líquido.

Un límite claro es la Tsal=231 K. Otro límite más aproximado es suponer que toda la energía que necesita el propano para atemperarse proviene del dedal. Podemos despreciar la contribución del gas frente a la del líquido.

>	eqBE:='mS*cS*(T0-TS)=rho*V*h[lv2]';cS:=subs(Sdat,c);rho:=subs(dat,rho);TS_:=subs(dat,solve(eqBE,TS)):'TS'=evalf(%,3);

¡Vaya!, parece que sobra frío. Conclusión, bastaría 1 cm3 de líquido para que el dedal se enfriase hasta la temperatura de ebullición del propano, y eso que la masa del dedal es casi 20 veces mayor. En realidad, resula dificilísimo medir el líquido que cae porque se vaporiza rápidamente. Si se pudiera medir la disminución de volumen de líquido interior en el recargador, habría que tener en cuenta que ya un 30% se vaporiza en el conducto de salida y 'no caería' sobre el dedal.

d) Índicar procedimientos que permitan determinar si el contenido es propano o butano.
De los más sencillos para distinguir líquidos es la gravimetría (medir la densidad y comparar con las tablas).

Para los gases licuados es mucho más sencillo medir la presión de vapor y comparar con las tablas.

Tal vez el más simple aquí sería dejar escapar un poco de líquido sobre una superficie y ver si se enfría un poco (butano) o mucho (propano).

Todos los líquidos puros, destilados, son incoloros, así que la colorimetría no sirve.

>