| > | restart:#"m06_p55" |
El CO2 se usa para carbonatar e impulsar la cerveza de barril, la cual se refrigera con una máquina aparte. Considérese una botella de 10 litros de CO2 que contiene 5 litros de líquido en equilibrio con su vapor a 20 ºC. Se pide:
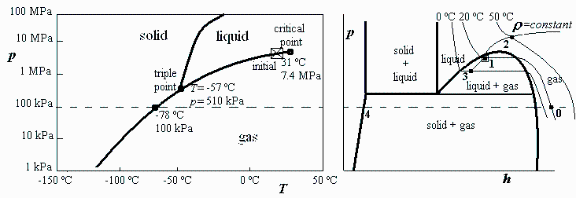
a) Hacer un esquema del diagrama p-T del CO2, indicando el estado interior y los valores de la presión y temperatura en el punto crítico y en el punto triple.
b) Hacer un esquema del diagrama p-h del CO2, indicando el estado interior.
c) Masa y presión inicial de CO2.
d) Indicar qué ocurre si la botella se pone en un ambiente a 50 ºC, y si se pone en un ambiente a 0 ºC.
e) Volumen de cerveza (considérese agua) que podría enfriarse 20 ºC, en un cambiador de calor con el CO2.
f) Volumen de cerveza (considérese agua) que podría elevarse 1,5 m de altura, utilizando convenientemente el CO2.
g) Cantidad de hielo seco que se podría generar utilizando convenientemente el CO2.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su1:="CO2":su2:="H2O":dat:=[V=0.01*m_^3,Vl=0.005*m_^3,T0=(20+273)*K_,Dz=1.5*m_,DT=-20*K_]; |
| > |
Eqs. const.:
| > | gdat:=get_gas_data(su1);ldat:=get_liq_data(su1);Wdat:=get_liq_data(su2):dat:=op(dat),gdat,ldat,Const,SI2,SI1:get_pv_data(su1):rho[CO2,liq]=subs(dat,rho); |
NOTA. Se va a usar el modelo de sustancia perfecta con los datos de las Tablas, pero la temperatura ambiente está tan cercana a la temperatura crítica del CO2, que el modelo de sustancia perfecta puede desviarse mucho del comportamiento real; e.g. la densidad del líquido saturado en el punto triple (-56 ºC, 518 kPa) es 1180 kg/m3, pero la del líquido saturado a 20 ºC (5,7 MPa) es 775 kg/m3.
a) Hacer un esquema del diagrama p-T del CO2, indicando el estado interior y los valores de la presin y temperatura en el punto crtico y en el punto triple.
| > | 'T[cr]'=subs(dat,T[cr]);'T[cr]'=TKC(rhs(%));'p[cr]'=subs(dat,p[cr]);Ttr:=subs(dat,T[f]):'T[tr]'=%;'T[tr]'=TKC(rhs(%));'p[tr]'='pv(T[tr])';ptr_:=subs(dat,evalf(subs(dat,pv(Ttr)))):'p[tr]'=evalf(%,2); |
i.e. se trata de un estado bifsico lquido-vapor, de una sustancia pura, cerca de su punto crtico, por lo que no valdrn los modelos de gases y lquidos perfectos. Usaremos el diagrama de la Fig. A3.4.
b) Hacer un esquema del diagrama p-h del CO2, indicando el estado interior.
c) Masa y presin inicial de CO2.
Despreciando la masa de vapor:
| > | eqm:=m=ml+mv;eqLIQ:=ml=rho*Vl;eqLIQ_:=subs(dat,eqLIQ):evalf(%,2);p1:='pv(T0)';p1_:=subs(dat,evalf(subs(dat,pv(T0)))):'p1'=evalf(%,2);eqVAP:=mv='p1*(V-Vl)/(Z*R*T0)';eqGRAF:=Z=0.5;eqVAP_:=mv=subs(eqGRAF,dat,p1_*(V-Vl)/(Z*R*T0)):evalf(%,2);eqx:=x=mv/(ml+mv);eqx_:=subs(eqLIQ_,eqVAP_,eqx):evalf(%,2); |
i.e. hay 5,9 kg de lquido y 1,0 kg de vapor, a 5,7 MPa.
d) Indicar qu ocurre si la botella se pone en un ambiente a 50 C, y si se pone en un ambiente a 0 C.
Si, con esa masa y ese volumen, el interior alcanza 50 C, la presin sera de 12 MPa, determinada por el cruce de la curva T=50 C con la curva rho_m=490 kg/m3 en el diagrama p-h del CO2, y todo sera fluido supercrtico. En la prctica, las botellas de CO2 suelen llevar una vlvula de seguridad por rotura de disco de cobre tarada a unos 15 MPa.
Si el interior alcanza 0 C, la presin sera de 3,5 MPa, determinada por el cruce de la curva T=0 C con la curva rho_m=490 kg/m3 en el diagrama p-h del CO2, y condensara un poco de vapor (ms de la mitad).
| > | eqVm:=rho_m=(ml+mv)/V;eqVm_:=subs(eqLIQ_,eqVAP_,dat,eqVm):evalf(%,2);p[2]:=12e6*Pa_;p[3]:=3.5e6*Pa_; |
e) Volumen de cerveza (considrese agua) que podra enfriarse 20 C, en un cambiador de calor con el CO2.
Supongamos que se va extrayendo gas, se expande isentlpicamente, se formar una neblina de hielo seco a -78 C, y se aprovecha hasta 20 C.
Del diagrama p-h del CO2 se toman los siguientes datos:
Estado 0 (20 C, 100 kPa): h=800 kJ/kg, s=4800 J/(kg.K)
Estado 1 (20 C, x=0,21): h=590 kJ/kg, s=3420 J/(kg.K)
Estado 1liq (20 C, x=0): h=560 kJ/kg, s=3330 J/(kg.K)
Estado 1vap (20 C, x=1): h=710 kJ/kg, s=3780 J/(kg.K)
Estado 4 (-78 C, 100 kPa): h=125 kJ/kg, s=1600 J/(kg.K)
| > | h[T20]:=800e3*J_/kg_;s[T20]:=4800*J_/(kg_*K_);h[bottle]:=590e3*J_/kg_;s[bottle]:=3420*J_/(kg_*K_);h[liq]:=560e3*J_/kg_;s[liq]:=3330*J_/(kg_*K_);h[aerosol]:=710e3*J_/kg_;s[aerosol]:=3780*J_/(kg_*K_);h[dryice]:=125e3*J_/kg_;s[dryice]:=1600*J_/(kg_*K_);eqBE:=0=m[CO2]*(h[T20]-h[aerosol])+m[H2O]*c*DT;eqBE_:=m[H2O]=subs(eqLIQ_,eqVAP_,Wdat,dat,-(ml+mv)*(h[T20]-h[aerosol])/(c*DT)):evalf(%,2); |
i.e. con los 6,9 kg de CO2 (5,9 de líquido+1 de gas) slo se enfriaran 7,5 kg de H2O, luego no resultar rentable y convendr usar un refrigerador externo en ciclo cerrado.
Si se hubiese usado el lquido directamente, dejando aparte el problema de la formacin de hielo seco que podra obstruir los conductos:
| > | eqBE:=0=m[CO2,liq]*(h[T20]-h[liq])+m[H2O]*c*DT;eqBE_:=m[H2O]=subs(eqLIQ_,Wdat,dat,-(ml)*(h[T20]-h[liq])/(c*DT)):evalf(%,2); |
i.e. usando directamente los 5,9 kg de lquido podran enfriarse 17 kg de agua.
El mximo vendra dado por las exergas.
Exerga necesaria para enfriar el agua:
| > | eqphi_H2O:=w[min,H2O]=c*DT-T0*c*ln((T0+DT)/T0);eqphi_H2O_:=subs(dat,evalf(subs(Wdat,dat,eqphi_H2O))):evalf(%,2); |
Exerga disponible en el CO2:
| > | i:='i':eqphi_CO2:=W[max,CO2]=DU+p0*DV-T0*DS;eqphi_CO2:=W[max,CO2]=H[f]-H[i]-p[f]*V[f]+p[i]*V[i]+p0*DV-T0*DS;eqphi_CO2:=W[max,CO2]=m*Dh+('p1'-p0)*V-T0*m*Ds;eqphi_CO2:=W[max,CO2]=subs(dat,evalf(subs(eqLIQ_,eqVAP_,dat,ml*(h[liq]-h[T20])+mv*(h[liq]-h[T20])-(p1_-p0)*V+T0*(ml+mv)*(s[T20]-s[bottle])))):evalf(%,2); |
i.e. como hay disponible 1 MJ y slo se necesitan 3 kJ/kg, se podra enfriar un mximo de 1000/3=333 kg de agua en el caso lmite. En la prctica ya resultara complicado conseguir enfriar los 17 kg antedichos, por lo que no se usa el CO2 para enfriar la cerveza.
f) Volumen de cerveza (considrese agua) que podra elevarse 1,5 m de altura, utilizando convenientemente el CO2.
La exerga necesaria es:
| > | eqphi_H2O:=w[min,H2O]=g*Dz;eqphi_H2O_:=subs(dat,eqphi_H2O):evalf(%,2);eq_:=m[H2O]=rhs(eqphi_CO2)/rhs(%):evalf(%,2); |
i.e. se necesita mucha menos energa para subir (bombear) que para refrigerar, por eso s se usa el CO2 para bombear la cerveza (adems de para carbonatarla, que es el objetivo principal) y sin embargo para enfriarla se usa una mquina refrigerante independiente.
La mayora de las cervezas de barril se carbonatan hasta disolver 2,5 volmenes de CO2 en condiciones de 100 kPa y 15 C en cada volumen de cerveza.
g) Cantidad de hielo seco que se podra generar utilizando convenientemente el CO2.
La exerga necesaria para obtener hielo seco es:
| > | i:='i':eqphi_dryice:=W[max,dryice]=DU+p0*DV-T0*DS;eqphi_dryice:=W[max,dryice]=H[f]-H[i]-p[f]*V[f]+p[i]*V[i]+p0*(V[f]-V[i])-T0*(S[f]-S[i]);eqphi_dryice:=W[max,dryice]=m*Dh+(p0-p0)*V-T0*m*Ds;eqphi_dryice:=W[max,dryice]=m[dryice]*subs(dat,evalf(subs(dat,h[dryice]-h[T20]-T0*(s[dryice]-s[T20])))):evalf(%,2);eqBX:=W[max,CO2]+W[max,dryice]=0;mdryice_:=subs(eqphi_dryice,eqphi_CO2,eqLIQ_,eqVAP_,W[max,CO2]/(W[max,dryice]/m[dryice])):'m[dryice]'=evalf(%,2); |
i.e. con la exerga de los 6,9 kg de CO2 iniciales (a 5.7 MPa), se podra conseguir congelar a 100 kPa 4,1 kg de CO2 hasta obtener hielo seco.
| > |