>	restart;#"m06_p48"

En una publicación se han encontrado los siguientes datos relativos a una botella de butano típica: diámetro exterior 0,300 m; altura total 0,459 m; capacidad 26,1 litros; masa en vacío 12,5 kg; carga de butano 12,5 kg, presión de prueba de resistencia 3 MPa; temperatura máxima permitida 50 ºC; sobrepresión de suministro a los aparatos de consumo (28±8) mb (milibares); gasto másico máximo que permite la válvula entre 0,5 kg/h y 1,5 kg/h, medible con un contador de hasta 4 m3/h (de los disponibles en el mercado, por si se quiere usar); poder calorífico mínimo del butano comercial 45 MJ/kg. Se pide:
a) Comprobar la compatibilidad de los datos geométricos y estimar el espesor de la pared con los datos apropiados de un acero (con esto y los datos elásticos se podría estimar la validez del dato estructural).
b) Con los datos apropiados del n-butano, comprobar que puede haber 12,5 kg en el interior.
c) Determinar el estado termodinámico interior para los casos previsibles de temperatura mínima de uso (tómese 10 ºC), normal (tómese 20 ºC), y máxima (tómese 50 ºC), comprobando que es compatible con la presión de suministro.
d) Comprobar la compatibilidad de los datos de caudal de la válvula y el caudalímetro.
e) Calcular la transmisión de calor necesaria para suministar el gasto másico máximo (con él y con los datos de transmitancia térmica a través de la pared se calcularía una mejor aproximación de la temperatura interior).
f) Calcular la potencia calorífica máxima suministrable y el caudal en litros/minuto de agua caliente sanitaria producible en un calentador a gas, tomando un salto de 15 ºC a 60 ºC.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="C4H10":su2:="H2O":su3:="Acero":dat:=[De=0.3*m_,L=0.459*m_,V=0.0261*m_^3,m0=12.5*kg_,m1=12.5*kg_,p9=1e6*Pa_,Tmax=(50+273)*K_,Dp=28*1e-3*1e5*Pa_,mdot1=(0.5/3600)*kg_/s_,mdot2=(1.5/3600)*kg_/s_,Cmax=(4/3600)*m_^3/s_,Tmin=(10+273)*K_,Tn=(20+273)*K_,PC=45e6*J_/kg_,DTw=(60-15)*K_];

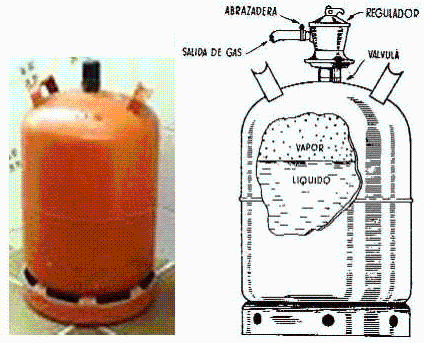
Fig. 1. Bombona de butano.

Eqs. const.:

>	g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=get_liq_data(su2):dat3:=get_sol_data(su3):pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

a) Comprobar la compatibilidad de los datos geométricos y estimar el espesor de la pared con los datos apropiados de un acero (con esto y los datos elásticos se podría estimar la validez del dato estructural).

>	Vcil:=L*Pi*De^2/4;Vcil_:=evalf(subs(dat,Vcil)):'Vcil_'=evalf(%,2);Aaprox:=Acil+2*Abase;Acil:=L*Pi*De+2*(Pi*De^2/4);Acil_:=subs(dat,Acil):'Acil_'=evalf(Acil_,2);Abase:=Pi*De^2/4;Abase_:=evalf(subs(dat,Abase)):'Abase'=evalf(%,2);eqM:=m0=rho*Aaprox*d;d:=subs(dat3,dat,solve(eqM,d)):'d_'=evalf(d,2);

Sí es posible que un recipiente inscrito en un volumen de 32 litros tenga 26 litros de capacidad.

Sí es posible que con esas dimensiones tenga 12,5 kg de masa, y, suponiendo espesor uniforme y un área aproximadamente igual al del cilindro envolvente, tendría casi 3 mm de espesor (3,2 +/- 0,2 mm según el catálogo).

Con 3 mm de espesor de acero un depósito cilíndrico sería capaz de aguantar una sobrepresión interior de Dp*D=2*sigma*d, que con sigma=300 MPa da Dp=18 MPa (en realidad, todas las botellas se prueban con agua a 3 MPa, y una al azar se comprueba que rompe a más de 9 MPa).

>	eqBF:=Dp*De='2*sigma*d';dat_ad:=sigma=300e6*Pa_;Dp_:=subs(dat_ad,dat,solve(eqBF,Dp)):'Dp'=evalf(%,2);

b) Con los datos apropiados del n-butano, comprobar que puede haber 12,5 kg en el interior.

>	mliq_max:=rho*V;mliq_max_:=subs(dat1,mliq_max):'mliq_max_'=evalf(%,2);

luego sí puede ser.

c) Determinar el estado termodinámico interior para los casos previsibles de temperatura mínima de uso (tómese 10 ºC), normal (tómese 20 ºC), y máxima (tómese 50 ºC), comprobando que es compatible con la presión de suministro.

>	p_int:='pv(T)';pTmax_:=evalf(subs(dat,pv1(Tmax))):'pTmax_'=evalf(%*kPa_/(1000*Pa_),2);pTn_:=evalf(subs(dat,pv1(Tn))):'pTn_'=evalf(%*kPa_/(1000*Pa_),2);pTmin_:=evalf(subs(dat,pv1(Tmin))):'pTmin_'=evalf(%*kPa_/(1000*Pa_),2);p_sum:=p0+Dp;p_sum_:=subs(dat1,p_sum):'p_sum_'=evalf(%*kPa_/(1000*Pa_),3);

En los 3 casos es mayor que la necesaria de suministro. Para determinar el estado, además de la presión hay que determinar el nivel o la fracción másica. Si no se cuenta la dilatación térmica el nivel apenas cambia (y aún así), por lo que se puede suponer que el vapor ocupa siempre el mismo volumen Vvap=V-mtot/rholiq.

>	Vliq:=m1/rho;Vliq_:=subs(dat1,Vliq):'Vliq_'=evalf(%,3);mvap:=p*(V-Vliq)/(R*T);x:='mvap/(mvap+mliq)';x_max_:=subs(p=pTmax_,T=Tmax,dat1,mvap/m1):'x_max_'=evalf(%,2);x_n_:=subs(p=pTn_,T=Tn,dat1,mvap/m1):'x_n_'=evalf(%,2);x_min_:=subs(p=pTmin_,T=Tmin,dat1,mvap/m1):'x_min_'=evalf(%,2);

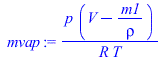d) Comprobar la compatibilidad de los datos de caudal de la válvula y el caudalímetro.

Supondremos que el caudal de mide a la presión de suministro y a la temperatura normal (no varía mucho con la T de trabajo).

>

mdot_max_:=evalf(subs(dat,mdot2),2);rho[gas_sum]:='p_sum/(R*T0)';rho[gas_sum]:=subs(dat1,rho[gas_sum]):'rho[gas_sum]'=evalf(%,2);mdot_cont:='rho[gas_sum]*Cmax';mdot_cont_:=subs(dat,%):'mdot_cont'=evalf(%,2);#rho0_:=subs(dat1,p0/(R*T0));mp_:=subs(dat1,C*rho);Qp:=mp*hlv*(1+vl/vv);Qp_:=subs(dat1,mp_*h[lv0]);

luego el caudalímetro sí sirve para medir el consumo.

e) Calcular la transmisión de calor necesaria para suministar el gasto másico máximo (con él y con los datos de transmitancia térmica a través de la pared se calcularía una mejor aproximación de la temperatura interior).

>	eqBE:=DE=Q+W+Int(h,m);Qdot:=mdot*h[lv]*(1+v[liq]/v[vap]);Qdot:=mdot*h[lv0];Qdot_:=subs(dat1,mdot_max_*h[lv0]):'Qdot_'=evalf(%,2);

f) Calcular la potencia calorífica máxima suministrable y el caudal en litros/minuto de agua caliente sanitaria producible tomando un salto de 15 ºC a 60 ºC.

>	Qdot_max:='mdot_max_*PC';Qdot_max_:=subs(dat1,%):'Qdot_max_'=evalf(%*kW_/(1000*W_),2);eqCAL:=Qdot_max*eta=mdot_ACS*c*DTw;mdot_ACS_:=subs(eta=1,dat2,dat1,solve(eqCAL,mdot_ACS)):'mdot_ACS_'=evalf(%,2);'mdot_ACS_'=evalf(rhs(%)*(litro_/kg_)*(60*s_/minuto_),2);

>