>	restart;#"m06_p45"

En un frasco Dewar de 250 cm3 hay inicialmente 50 cm3 de agua pura en equilibrio con su vapor a 98 ºC. A partir de un cierto instante se empieza a extraer vapor con una bomba de vacío. Se pide:
a) Esquema de la instalación, estado inicial y esquema general de las fases del agua en los diagramas p-T y T-s.
b) Determinar la presión, la temperatura, la masa de vapor interior y la masa de vapor evacuada desde el instante inicial, en el momento en que empieza a formarse hielo.
c) Determinar la presión, la temperatura, la masa de vapor interior y la masa de vapor evacuada desde el instante inicial, en el momento en que desaparece al agua líquida.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":dat:=[V=250e-6*m_^3,V1=50e-6*m_^3,T1=(98+273)*K_];

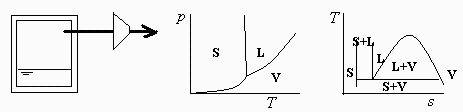
Esquema:

>

>

Eqs. const.:

>	eqETg:=eq1_9;eqEE:=eq1_10;gdat:=get_gas_data(su):ldat:=get_liq_data(su):dat:=op(dat),gdat,ldat,Const,SI2,SI1:get_pv_data(su):

a) Esquema de la instalación, estado inicial y esquema general de las fases del agua en los diagramas p-T y T-s.

>	p1_:=subs(dat,evalf(subs(dat,pv(T1)))):'p1'=evalf(%,2);m1:=rho*V1;m1_:=subs(dat,m1):'m1'=evalf(%,2);rho_:=subs(dat,rho):'rho'=evalf(%,2);

aunque a 98 ºC es rho=960 kg/m3.

b) Determinar la presión, la temperatura, la masa de vapor interior y la masa de vapor evacuada desde el instante inicial, en el momento en que empieza a formarse hielo.
Despreciando la masa gaseosa:

>	T2:=T[tr];p2_:=subs(dat,evalf(subs(dat,pv(T2)))):'p2'=evalf(%,2);eqBEaprox:=m*c*dT-h[lv0]*dm=0;m:=m1*exp(c*(T-T1)/h[lv0]);m2_:=evalf(subs(dat,T=T2,dat,m)):'m2'=evalf(%,2);mvint:=p*(V-V1)/(R*T);mvint_:=subs(dat,p2_*(V-V1)/(R*T2)):'mvint'=evalf(%,2);

c) Determinar la presión, la temperatura, la masa de vapor interior y la masa de vapor evacuada desde el instante inicial, en el momento en que desaparece al agua líquida.

>	T3:=T[tr];p3_:=subs(dat,evalf(subs(dat,pv(T3)))):'p3'=evalf(%,2);eqBEaprox:=ms*h[sl0]-mv*h[lv0]=0;eqBM:=ms+mv=m2_:evalf(%,2);sol1:=subs(dat,solve({eqBEaprox,eqBM},{ms,mv})):'mv'=evalf(subs(sol1,mv),2);

>