>	restart;#"m06_p41"

En un matraz de 250 cm3 se echa 150 cm3 de agua ambiente (a 15 ºC) y, sin tapar, se lleva a ebullición, tapándose en ese momento y apartándose del foco calorífico. Se pide:
a) Aumento de volumen suponiendo un coeficiente medio de dilatación de 5×10-4 K-1 y despreciando la evaporación.
b) Masa de vapor en el instante de cierre y una vez atemperado todo.
c) Tiempo que tarda en enfriarse hasta 45 ºC, suponiendo que la pérdida de calor es proporcional a la diferencia entre la temperatura interior y la exterior,  , con un valor UA=1 W/K, considerando que la temperatura interior es uniforme y la masa de vidrio pequeña.
d) ¿Qué ocurrirá en el interior si en ese momento se pone el matraz debajo de un chorro de agua ambiente (enfriándose antes el vapor que el líquido por su menor inercia térmica)?
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":dat:=[V=250e-6*m_^3,V1=150e-6*m_^3,alpha=5e-4/K_,T3=(45+273)*K_,UA=1*W_/K_];

Esquema:

>

>

Eqs. const.:

>	eqETl:=rho=rho0*(1-alpha*(T-T0));eqETg:=eq1_9;eqEE:=eq1_10;gdat:=get_gas_data(su):ldat:=get_liq_data(su):dat:=op(dat),gdat,ldat,Const,SI2,SI1:get_pv_data(su):

a) Aumento de volumen suponiendo un coeficiente medio de dilatación de 5×10-4 K-1 y despreciando la evaporación.

>	p2:=p0;V2:=V1*(1+alpha*(T2-T0));T2_:=subs(dat,solve(subs(dat,p2=pv(T)),T)):'T2'=evalf(%,3);V2_:=subs(dat,T2=T2_,V2):'V2'=evalf(%,2);DV_:=subs(dat,V2_-V1):'DV'=evalf(%,2);

b) Masa de vapor en el instante de cierre y una vez atemperado todo.

>	mv2:=rho2*(V-V2);mv2_:=subs(dat,(p2/(R*T2_))*(V-V2_)):'mv2'=evalf(%,2);p3:=pvT0;p3_:=subs(dat,evalf(subs(dat,pv(T0)))):'p3'=evalf(%,2);mv3:=rho3*(V-V1);mv3_:=subs(dat,(p3_/(R*T0))*(V-V1)):'mv3'=evalf(%,2);Dm_:=mv3_-mv2_:'Dm'=evalf(%,2);

¿Ojo! que aunque parece que aumentaría el nivel al atemperarse no se ha tenido en cuenta la evaporación.

c) Tiempo que tarda en enfriarse hasta 45 ºC, suponiendo que la pérdida de calor es proporcional a la diferencia entre la temperatura interior y la exterior,  , con un valor UA=1 W/K, considerando que la temperatura interior es uniforme y la masa de vidrio pequeña.

Casi todo es líquido, luego basta tomar su variación de energía.

>

eqBE_:=m*c*diff(T(t),t)=-UA*(T(t)-T0);sol1:=dsolve({eqBE_,T(0)=T2},T(t));m1_:=subs(dat,rho*V1):'m1'=evalf(%,2);T_:=subs(dat,T2=T2_,m=m1_,rhs(sol1)):'T'=evalf(%,2);t45_:=solve(subs(dat,T_=T3),t):'t45'=evalf(%,2);plot([[[0,subs(dat,T0/K_)],[1000,subs(dat,T0/K_)]],[[0,subs(dat,T3/K_)],[t45_/s_,subs(dat,T3/K_)]],subs(SI0,T_)],t=0..1000,Temp=273..373,color=black);

>

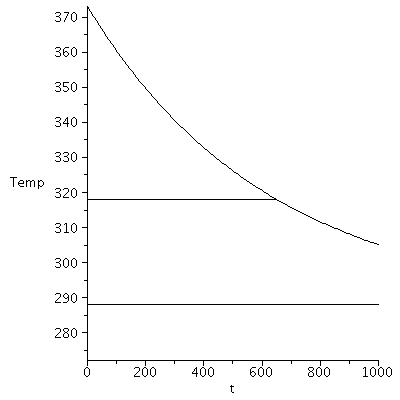d) ¿Qué ocurrirá en el interior si en ese momento se pone el matraz debajo de un chorro de agua ambiente (enfriándose antes el vapor que el líquido por su menor inercia térmica)?

Que al enfriarse el vapor a V=cte disminuiría la presión más rápido que la T porque también condensaría) y, al estar el líquido a T>Tv herviría, i.e. se generarían burbujas hasta restablecer la pv45.