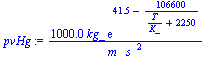>	restart;#"m06_p40"

Se trata de comprobar la coherencia o consistencia de los datos termodinámicos que figuran en las siguientes notas históricas:
Nota 1: En 1644, dos años después de la muerte de Galileo, su discípulo Torricelli fue el primero en medir la presión atmosférica, que en Florencia (49 m sobre el nivel del mar) resultaba equivalente a la de una columna de 760±4 mm de mercurio con vacío por arriba. Tras conocerse esto en París,, en 1647 Pascal instó a un cuñado suyo a medir la altura barométrica al pie de una montaña y a 1000 m de altitud sobre ese terreno, resultando ser de 663 mm y 586 mm de mercurio, respectivamente.
Nota 2: En 1740, Fahrenheit en Holanda perfeccionó tanto el termómetro de capilar de mercurio que descubrió que la temperatura de ebullición de las sustancias variaba con la presión atmosférica y llegó a proponer a la Royal Society de Londres utilizar su termómetro como hipsómetro (es decir, como medidor de altitudes geográficas), midiendo la temperatura de ebullición local del agua.
Se pide:
a) Calcular el valor y la incertidumbre de la presión a nivel del mar (en el Sistema Internacional), suponiendo que g=9,80±0,01 m/s2 y que la densidad del mercurio es de 13560±30 kg/m3.
b) Calcular la presión del vacío del barómetro a 20 ºC y la temperatura de ebullición normal, sabiendo que los coeficientes de la ecuación de Antoine, lnp=A-B/(C+T), para el mercurio son A=41,5, B=107000 y C=2250, con p en kPa y T en K.
c) Estimar la densidad del aire ambiente a partir de los datos del barómetro, así como la altitud sobre el nivel del mar al pie de la montaña mencionada.
d) Estimar la resolución del hipsómetro de Fahrenheit sabiendo que él garantizaba una resolución de 0,5 ºC. ¿Y si se midiese la ebullición del etanol en lugar de la del agua?
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Hg":su2:="Aire":su3:="H2O":su4:="C2H6O":dat:=[z0=0.760*m_,Dz0=4e-3*m_,Dz12=1000*m_,z1=0.663*m_,z2=0.586*m_,g=9.8*m_/s_^2,Dg=0.01*m_/s_^2,rho[Hg]=13560*kg_/m_^3,Drho[Hg]=30*kg_/m_^3,T0=293*K_,A=41.5,B=106600,C=2250,DT=0.5*K_];

Esquema:

>

>

Eqs. const.:

>

eqETg:=eq1_11;eqEE:=eq1_16;gdat:=get_gas_data(su2):gdatH2O:=get_gas_data(su3):gdatC2H6O:=get_gas_data(su4):ldatHg:=get_liq_data(su1):ldatH2O:=get_liq_data(su3):ldatC2H6O:=get_liq_data(su4):dat:=op(dat),gdat,Const,SI2,SI1:get_pv_data(su4):pvC2H6O:=pv(T);get_pv_data(su3):'pv(T)'=pv(T);pvHg:=subs(dat,1e3*Pa_*exp(A-B/(T/K_+C)));

a) Calcular el valor y la incertidumbre de la presión a nivel del mar (en el Sistema Internacional), suponiendo que g=9,80±0,01 m/s2 y que la densidad del mercurio es de 13560±30 kg/m3.

>	p0:=rho[Hg]*g*z0;p0_:=subs(dat,subs(dat,ldatHg,rho*g*z0)):'p0'=evalf(%,2);Dp0:=p0*(Drho[Hg]/rho[Hg]+Dg/g+Dz0/z0);Dp0_:=subs(dat,subs(dat,ldatHg,p0_*(Drho[Hg]/rho+Dg/g+Dz0/z0))):'Dp0'=evalf(%,2);

b) Calcular la presión del vacío del barómetro a 20 ºC y la temperatura de ebullición normal, sabiendo que los coeficientes de la ecuación de Antoine, lnp=A-B/(C+T), para el mercurio son A=41,5, B=106600 y C=2250, con p en kPa y T en K.

>	pvHg20_:=subs(dat,evalf(subs(T=T0,dat,pvHg))):'pvHg20'=evalf(%,2);TvHg100_:=subs(dat,solve(subs(dat,p0_=pvHg),T)):'TvHg100'=evalf(%,2);

c) Estimar la densidad del aire ambiente a partir de los datos del barómetro, así como la altitud sobre el nivel del mar al pie de la montaña mencionada.

>	eq12:=Dp12=rho*g*Dz12;eq12:=rho[Hg]*g*(z1-z2)=rho*g*Dz12;rho_:=subs(dat,solve(subs(dat,eq12),rho)):'rho'=evalf(%,2);eq01:=rho[Hg]*g*(z0-z1)=rho*g*Dz01;Dz01_:=subs(rho=rho_,dat,solve(subs(dat,eq01),Dz01)):'Dz01'=evalf(%,2);

d) Estimar la resolución del hipsómetro de Fahrenheit sabiendo que él garantizaba una resolución de 0,5 ºC. ¿Y si se midiese la ebullición del etanol en lugar de la del agua?

Por Antoine, numérico:

>	pvW100_:=subs(ldatH2O,pv(T[b])):'pvW100'=evalf(%,2);pvW99_:=subs(ldatH2O,pv(T[b]-1*K_)):'pvW99'=evalf(%,2);Dpv_T100:=(pv100-pv99)/K_;Dpv_T100_:=(pvW100_-pvW99_)/(1*K_):'Dpv_T100'=evalf(%,2);eq1:=Dpv=rho*g*Dz;Dz_:=subs(Dpv=Dpv_T100_*DT,rho=rho_,dat,solve(eq1,Dz)):'Dz'=evalf(%,2);

Por Clapeyron, analítico:

>	eqC:=Dpv_T=h[lv0]/(R*T^2/p);Dpv_T100_:=subs(T=T[b],p=p0_,gdatH2O,ldatH2O,h[lv0]/(R*T^2/p)):'Dpv_T100'=evalf(%,2);Dz_:=subs(Dpv=Dpv_T100_*DT,rho=rho_,dat,solve(eq1,Dz)):'Dz'=evalf(%,2);

Etanol:

No se gana nada porque aunque la hlv es menor, la R es mayor

>	Dpv_T100_:=subs(T=T[b],p=p0_,gdatC2H6O,ldatC2H6O,h[lv0]/(R*T^2/p)):'DpvT100'=evalf(%,2);Dz_:=subs(Dpv=Dpv_T100_*DT,rho=rho_,dat,solve(eq1,Dz)):'Dz'=evalf(%,2);

>