>	restart;#"m6_p32"

Un recipiente cilíndrico vertical, cerrado y rígido, de 1 m de diámetro y 1 m de altura, contiene inicialmente 715 litros de agua líquida en equilibrio a 120 ºC con su vapor. Sabiendo que la presión interna no debe pasar de 4 MPa, se pide:
a) Presión y fracción másica inicial de vapor.
b) Temperatura máxima a que puede calentarse el agua.
NOTA: El volumen específico del agua líquida a 120 ºC es 1,06.10-3 m3/kg, su coeficiente de expansión es 0,9.10-3 K-1 (y crece casi linealmente, siendo 1,9.10-3 K-1 a 250 ºC), y su coeficiente de compresibilidad es 4,5.10-10 Pa-1.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":dat:=[Di=1*m_,L=1*m_,Vliq1=0.715*m_^3,T1=(120+273)*K_,p2=4e6*Pa_,v120=1.06e-3*m_^3/kg_,T120=(120+273)*K_,alpha120=0.9e-3/K_,T250=(250+273)*K_,alpha250=1.9e-3/K_]:dat:=[op(dat),A=evalf(subs(dat,Pi*Di^2/4))]:dat:=[op(dat),V=subs(dat,A*L)]:evalf(%,2);

Esquema:

>

>

Eqs. const.:

>

eqETg:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su):ldat:=get_liq_data(su):eqETl:=dv/v=alpha*dT;eqETl:='d||rho/rho'=-alpha*dT;alpha:=a+b*T;eqETl:=rho=rho0*exp(-a*(T-T0)-(b/2)*(T^2-T0^2));alpha:=alpha120+(alpha250-alpha120)*(T-T120)/(T250-T120);rho(T):=1/v120*exp(-(alpha120-(alpha250-alpha120)/(T250-T120)*T120)*(T-T120)-(alpha250-alpha120)/(T250-T120)*(T^2-T120^2)/2);plot(subs(dat,SI0,rho(T)),T=120+273..250+273,'rho'=800..1000);dat:=op(dat),gdat,ldat,Const,SI2,SI1:get_pv_data(su):

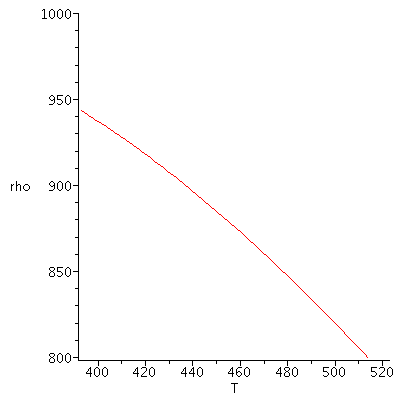a) Presión y fracción másica inicial de vapor.

>	p1_:=subs(dat,evalf(subs(dat,pv(T1)))):'p1'=evalf(%,2);mliq1_:=evalf(subs(dat,T=T1,dat,rho(T)*Vliq1)):'mliq1'=evalf(%,2);mvap1_:=subs(Z=1,p=p1_,T=T1,V=V-Vliq1,dat,solve(eqETg,m)):'mvap1'=evalf(%,2);m_:=mliq1_+mvap1_:'m'=evalf(%,2);x1_:=mvap1_/m_:'x1'=evalf(%,2);

b) Temperatura máxima a que puede calentarse el agua.

Como la masa de vapor es despreciable, cuando la dilatación de la masa de líquido ocupe todo el volumen.

>	eqVfull:=V=m/'rho(T)';eqVfull_:=subs(dat,V=m_/rho(T));Tmax_:=evalf(solve(eqVfull_,T))[1]:'Tmax'=evalf(%,2);

>
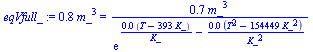