>	restart;#"m6_p21"

Con una botella de 30 litros que contiene inicialmente 8 kg de propano en un ambiente a 0 °C, se quiere suministrar gas a 1,4 MPa, para lo cual se instala un calentador en su interior. Suponiendo que el intercambio de calor con el ambiente se puede suponer dado por  = A(Tamb Tprop) con A = 8 W/K, y aproximando la presión de vapor en variables reducidas por la expresión ln prR= B(1 1/TR) con B = 6. Se pide:

a)•Determinar, con la expresión anterior, la presión inicial, la temperatura a la que habrá que calentar la botella y la entalpía de vaporización.

b)•Densidades del vapor saturado a 0 °C y a 1,4 MPa.

c)•Sabiendo que el calentador es de 1500 W, indicar cómo se calcularía el tiempo que se tarda en alcanzar los 1,4 MPa.

d)•Calcular el gasto inicial si al alcanzar los 1,4 MPa se abre la botella.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="C3H8":dat:=[V1=0.03*m_^3,m1=8*kg_,T1=(0+273)*K_,p2=1.4e6*Pa_,A=8*W_/K_,B=6,Qin=1500*W_];Qout:=A*(Tin-T0_);eqPV:=ln(p/p[cr])=B*(1-T[cr]/T);

Esquema:

>

>

Eqs. const.:

>	eqET:=subs(eq1_11,rho=p/(Z*R*T));eqEE:=eq1_16;gdat:=get_gas_data(su):ldat:=get_liq_data(su):dat:=op(dat),Const,gdat,ldat,SI2,SI1:get_pv_data(su):T[cr]=subs(dat,T[cr]),p[cr]=evalf(subs(dat,p[cr])/(1e6*Pa_/MPa_),3);

a)•Determinar, con la expresión anterior, la presión inicial, la temperatura a la que habrá que calentar la botella y la entalpía de vaporización.

>

p1_:=subs(dat,solve(subs(dat,T=T1,dat,eqPV),p)):'p1'=evalf(%/(1e3*Pa_/kPa_),3);p1_Ant_:=subs(dat,evalf(subs(dat,T=T1,dat,pv(T)))):'p1_Ant'=evalf(%/(1e3*Pa_/kPa_),3);T2_:=solve(subs(dat,p=p2,dat,eqPV),T):'T2'=evalf(%,3);T2_Ant_:=subs(dat,evalf(subs(dat,solve(p2=pv(T),T)))):'T2_Ant'=evalf(%,3);eqPVclap_:=subs(p[0]=p[cr],T[0]=T[cr],eq6_4);sol1:=solve({eqPV,eqPVclap_},{B,p[cr]});hlv_:=subs(dat,solve(B=subs(sol1,B),h[lv])):'hlv'=evalf(%/(1e3*J_/kJ_),3);

b)•Densidades del vapor saturado a 0 °C y a 1,4 MPa.

>

pR1_:=subs(dat,p1_/p[cr]):'pR1'=evalf(%,2);TR1_:=subs(dat,T1/T[cr]):'TR1'=evalf(%,2);Z1_:=0.88;pR2_:=subs(dat,p2/p[cr]):'pR2'=evalf(%,2);TR2_:=subs(dat,T2_/T[cr]):'TR2'=evalf(%,2);Z2_:=0.77;rho1_:=subs(Z=Z1_,p=p1_,T=T1,dat,rhs(eqET)):'rho1'=evalf(%,3);rho2_:=subs(Z=Z2_,p=p2,T=T2_,dat,rhs(eqET)):'rho2'=evalf(%,3);

c)•Sabiendo que el calentador es de 1500 W, indicar cómo se calcularía el tiempo que se tarda en alcanzar los 1,4 MPa.

Tomo como referencia el líquido a T1 y p1=pvT1.

>	eqBE12:=m*(uliq2+x2*(hlv2-p2*vlv2)-uliq1-x1*(hlv1-p1*vlv1))=Q;U:='U':deq:=diff(U(t),t)=Qin-A*(T(t)-T0);Uini:=0+x1*m1*ulv1;Uini:=0+x1*m1*(hlv1-p1*vlv1);U:=(1-x)*m1*c*(T-T1)+x*m1*(hlv1-p1*vlv1+c[v]*(T-T1));U:=(1-x)*m1*c*(T-T1)+x*m1*(hlv1-R*T1+(c[p]-R)*(T-T1));

Para una primera estimación se supone que no se vaporiza nada (x=0) y que la T varía linealmente:

>	Uuno:=subs(x=0,U);T:=T1+(T2-T1)*(t/t12);dequno:=diff(Uuno,t)=subs(t=t12/2,Qin-A*(T-T0));t12_:=subs(T2=T2_,dat,solve(dequno,t12)):'t12'=evalf(%,2);T:='T':

Para una segundaa estimación se supone que no se vaporiza nada y que la Qout varía linealmente:

>	Udos:=subs(x=0,U);deqdos:=diff(m1*c*(T(t)-T1),t)=subs(T=T1+(T2-T1)*(t/t12),Qin-A*(T-T0));dsol:=dsolve({deqdos,T(0)=T1},T(t));t12_:=subs(dat,T2=T2_,dat,solve(T2_=subs(t=t12,rhs(dsol)),t12)):'t12'=evalf(%,2);

Se observa que la T(t) es cuadrática, pero casi lineal.

Para una terceraa estimación se supone que no se vaporiza nada, pero T y Qout no lineales:

>	Utres:=subs(x=0,U);deqtres:=diff(m1*c*(T(t)-T1),t)=Qin-A*(T(t)-T0);dsol:=dsolve({deqtres,T(0)=T1},T(t));t12_:=evalf(subs(dat,T2=T2_,dat,solve(T2_=subs(t=t12,rhs(dsol)),t12))):'t12'=evalf(%,2);

Se observa que la T(t) es exponencial, pero casi lineal.

Para una cuarta estimación se considera ya la vaporización, pero T(t) lineal:

>

T:='T':pv:='pv':x:='x':'U'=U;x_:=(V1/m1-1/rho)/(Z*R*T/pv-1/rho);x_:=V1/m1/(R*T/pv);pv_:=p0*exp((-h[lv0]/R)*(1/T-1/T0));T:=T1+(T2-T1)*(t/t12);pvlin_:=evalf(subs(dat,T2=T2_,convert(series(pv_,t=0,2),polynom))):'pvlin_'=evalf(%,2);xlin_:=evalf(subs(dat,T2=T2_,convert(series(subs(pv=pvlin_,x_),t=0,2),polynom))):'xlin_'=evalf(%,2);Ulin_:=convert(series(subs(x=xlin_,hlv1=h[lv0],dat,T2=T2_,U),t=0,2),polynom):'Ulin'=evalf(%,2);deqlin:=diff(Ulin_,t)=subs(T=T1+(T2-T1)*(t/t12),t=t12/2,dat,SI2,T2=T2_,Qin-A*(T-T0)):'deqlin_'=evalf(%,2);t12_:=subs(dat,solve(deqlin,t12)):'t12'=evalf(%,2);

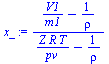La solución exacta se obtendría numéricamente.

d)•Calcular el gasto inicial si al alcanzar los 1,4 MPa se abre la botella.

>	mdot:=Qdot/h[lv0];mdot_:=subs(dat,Qin/h[lv0]):'mdot'=evalf(%,2);

>