>	restart:#"m05_p51"

Se quiere comprimir 0,1 kg/s de CO2 desde las condiciones ambiente de 15 ºC y 95 kPa, hasta 900 kPa. Se pide:
a) Temperatura de salida que supondría un consumo mínimo.
b) Consumo mínimo (límite termodinámico).
c) Consumo mínimo usando un compresor adiabático.
d) Indicar en un diagrama p-v el área que correspondería al trabajo unitario necesario (i.e. pdv o vdp).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="CO2":dat:=[mdot=0.1*kg_/s_,p0=95e3*Pa_,p1=900e3*Pa_];

Ecs. const.:

>	dat:=op(dat),get_gas_data(su),Const,SI2,SI1:

a) Temperatura de salida que supondría un consumo mínimo.

Aplicaremos el modelo de gas perfecto, pues las correcciones por compresibilidad son pequeñas (en el estado más desfavorable, a alta p y baja T, es Z=0,95).

>	pR_1:=subs(dat,p1/p[cr]);TR_0:=subs(dat,T0/T[cr]);

La Tsalida óptima sera la Tamb, porque tanto calentar como enfriar costaría más energía.

Demostración: por unidad de gasto,

>	w[min]:=c[p]*(T1-T0)-T0*(c[p]*ln(T1/T0)-R*ln(p1/p0));eq1:=Diff(w[min],T1)=0;eq1_:=diff(w[min],T1)=0;T1opt:=solve(diff(w[min],T1)=0,T1);

b) Consumo mínimo (límite termodinámico).

>	Wdot_min:=mdot*Dpsi;Wdot_min:=mdot*(Dh-T0*Ds);Wdot_min:=mdot*(c[p]*(T2-T1)-T0*(c[p]*ln(T2/T1)-R*ln(p2/p1)));Wdot_min_:=subs(dat,evalf(subs(T1=T0,T2=T0,p1=p0,p2=p1,dat,%)));

i.e. como mínomo 12 kW.

c) Consumo mínimo usando un compresor adiabático.

>	Wdot:=mdot*Dh;Wdot:=mdot*c[p]*(T2-T1);T2min:=T1*(p2/p1)^((gamma-1)/gamma);T2min_:=subs(T1=T0,p1=p0,p2=p1,dat,%);Wdot_:=subs(T1=T0,T2=T2min_,p1=p0,p2=p1,dat,Wdot);

i.e., casi 16 kW.

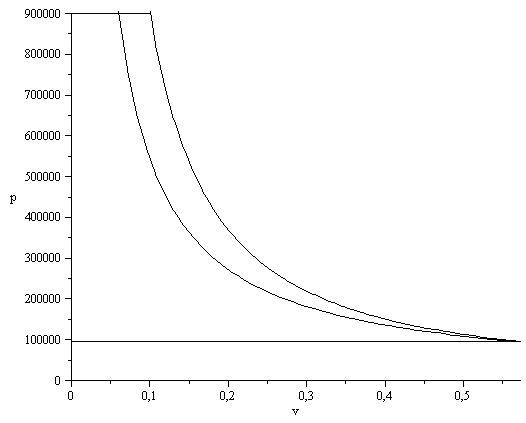
d) Indicar en un diagrama p-v el área que correspondería al trabajo unitario necesario (i.e. pdv o vdp).

De la ecuación de Bernoulli generalizada se deduce que, si no hay variación de energía mecánica ni fricción, w=Int(v,p).

>	eqBern:=w=Int(v,p)+De[m]+e[mdf];w=Int(v,p0..p1);

La explicación es que el trabajo termodinámico se define como dW=-pdV (o dw=-pdv por unidad de masa) PARA UNA MASA DE CONTROL, y aquí, para un volumen de control, el símbolo 'w' se refiere al trabajo que hay que comunicar al fluido circulante sólo A TRAVÉS DEL CONTORNO IMPERMEABLE, habiéndose combinado el trabajo de flujo con la energía para formar la entalpía.

>	v0:=R*T0/p0;v0_:=subs(dat,%);v1exe:=R*T0/p1;v1exe_:=subs(dat,%);v1adi:='v0*(p0/p1)^(1/gamma)';vadi_:=subs(dat,%);

>	plot(subs(dat,SI0,{[[0,subs(dat,SI0,p0)],[subs(dat,SI0,v0),subs(dat,SI0,p0)]],[[0,subs(dat,SI0,p1)],[subs(SI0,vadi_),subs(dat,SI0,p1)]],p0*(v0/v)^gamma,v0*p0/v}),v=0..subs(dat,SI0,v0),p=0..subs(dat,SI0,p1),color=black);

>