>	restart:#"m05_p50"

Entra 1 kg/s de vapor en una turbina a 4,5 MPa y 400 ºC. Sabiendo que sale saturado, se pide:
a) Presión de salida, y densidades de entrada y salida, con ayuda del diagrama de Mollier.
b) Trabajo específico y potencia producida.
c) Cálculo de la densidad, entalpía y entropía específicas en el estado inicial, con el modelo de sustancias perfectas.
d) Cálculo del estado final con el modelo de sustancias perfectas.
e) Calcular la capacidad térmica específica del vapor en el estado inicial con ayuda del diagrama de Mollier.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="H2O":dat:=[m=1*kg_/s_,p1=4.5e6*Pa_,T1=(400+273.15)*K_];

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Presión de salida, y densidades de entrada y salida, con ayuda del diagrama de Mollier.

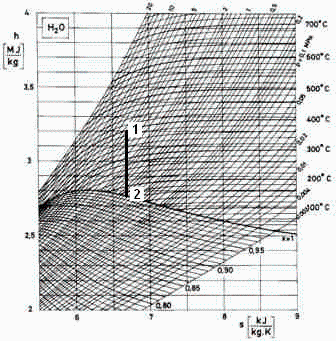
Basta bajar por la vertical del punto 1 (que es donde se cruzan la p1 y la T1), hasta llegar a la curva de vapor saturado, obteniéndose p2=0,7 MPa (y T2=165 ºC). Se observa que ambos puntos están en zonas donde las isotermas dejan de ser horizontales, indicando que las correcciones sobre el modelo de gas ideal pueden ser importantes.

Para las densidades, como no vienen explícitamente en el diagrama de Mollier usado, se procede al cálculo gráfico rho=Dp/Dh a s=cte.

>

p2_:=0.7e6*Pa_;T2_:=(165+273.15)*K_;eqh:=dh=T*ds+v*dp;v=Diff(h,p)[s];eqrho:=rho=(Dp/Dh)[s];eqrho1:=rho1=(`p1''`-`p1'`)/(`h1''`-`h1'`);eqrho1:=rho1=subs(dat,(6.2e6-3.2e6)*Pa_/((3.3e6-3.1e6)*J_/kg_));eqrho2:=rho2=subs(dat,(1.0e6-0.5e6)*Pa_/((2.83e6-2.69e6)*J_/kg_));eqrhoMGP:=rho1[MGP]=p1/(R*T1);subs(dat,%);eqrhoMGP:=rho2[MGP]=p2/(R*T2);subs(p2=p2_,T2=T2_,dat,%);

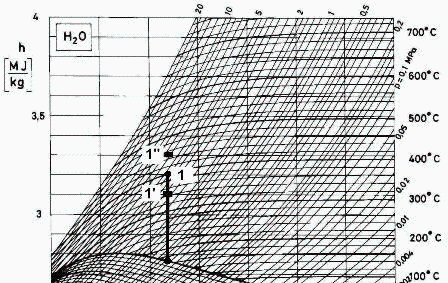
como se ve, puede ser aceptable la aproximación de gas ideal pese a la curvatura de las isotermas en esa zona, sobre todo por la gran incertidumbre del cálculo gráfico. Los valores más exactos son: rho1=15,44 kg/m3 y rho2=3.67 kg/m3.

b) Trabajo específico y potencia producida.

Mirando las entalpías en el diagrama:

>	eqBE:=q+w=Dh[t];w:=h1-h2;w_:=(3.21e6-2.76e6)*J_/kg_;Wt:='m*w';Wt_:=subs(w=w_,dat,%);

i.e. la turbina de vapor daría 450 kW (en realidad, tendrá un rendimiento isoentrópico que no llegará al 90%, disminuyendo proporcionalmente la potencia de salida). Este tipo de turbinas cuya salida no es a un condensador en vacío, se denominan turbinas a contrapresión, y se usan en cogeneración (generación de trabajo y de 'vapor vivo' para dar calor en otros procesos.

c) Cálculo de la densidad, entalpía y entropía específicas en el estado inicial, con el modelo de sustancias perfectas.

Las densidades ya lo hemos hecha antes. Para las entalpías y entropías hace falta elegir un estado de referencia, que, para que coincida con el del diagrama de Mollier usado, se elige h=0 y s=0 para el líquido en el punto triple, como de costumbre.

>	eqrhoMGP:=rho1[MGP]=p1/(R*T1);subs(dat,%);h=hv(T);h1_:=subs(dat,T=T1,dat,hv(T));s=sv(T,p);s1_:=subs(dat,evalf(subs(dat,T=T1,p=p1,dat,sv(T,p))));

que se compara favorablemente con los valores del gráfico: h1=3,2 MJ/kg y s1=6,7 kJ/kg·K).

d) Cálculo del estado final con el modelo de sustancias perfectas.

Habrá que hallar antes el punto 2 con este modelo, imponiendo la condición de isentropía y la de saturación.

>

p2:='p2':T2:='T2':eq1:=s2=s1;eq2:=p2=p[v](T2);p2:=pv(T2);eq1:=s2=subs(dat,T=T2,p=p2,dat,sv(T,p)):eq0:=f(T2)=s1-s2;eq0:=f(T2)=subs(SI0,s1_-rhs(eq1));eq0_:=evalf(subs(T2=400,eq0));eq0__:=evalf(subs(T2=500,eq0));T2_:=fsolve(subs(SI0,s1_=rhs(eq1)),T2=300..600)*K_;p2_:=evalf(subs(T2=T2_,p2));h2_:=subs(dat,T=T2_,dat,hv(T));s2_:=subs(dat,evalf(subs(dat,T=T2_,p=p2_,dat,sv(T,p))));w_:=h1_-h2_;Wt_:=subs(w=w_,dat,Wt);

i.e. el modelo de sustancia perfecta no es muy bueno, errando bastante la presión de salida (cambia de 0,70 MPa a 0,81 MPa), pero la aproximación es buena para la potencia.

e) Calcular la capacidad térmica específica del vapor en el estado inicial con ayuda del diagrama de Mollier.

Se puede hacer como cp=Dh/DT a p=cte, o como cp=TDs/DT a p=cte.

>	eqcp:=c[p]=Diff(h,T)[p];eqcp:=c[p]=(Dh/DT)[p];eqcp:=c[p1]=(`h1''`-`h1'`)/(`T1''`-`T1'`);eqcp:=c[p]=(3.3e6-3.1e6)*(J_/kg_)/((440-355)*K_);

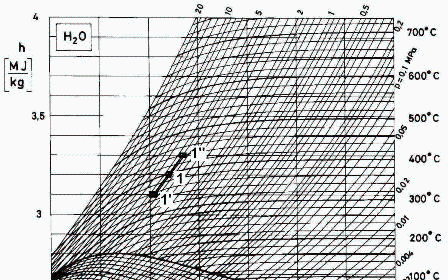
que se compara favorablemente con el mejor valor disponible: cp=2419 J/(kg·K). Nótese que el modelo de sustancia perfecta mantendría un cp=cte para el vapor, y en realidad varía bastante con la temperatura y la presión (cp(T2,p2)=2414 J/(kg·K)).

>