>	restart:#"m05_p47"

A un cierto dispositivo entra aire a 20 ºC y 200 kPa, estando el ambiente a 20 ºC y 100 kPa. Se pide:
a) Se desea saber si es posible que, sin necesidad de otras fuentes de energía, se puede conseguir que salgan dos flujos de aire a 100 kPa, uno de fracción másica , a 100 ºC y otro (1- a 0 ºC. Hacer un esquema y justificar mediante las ecuaciones apropiadas si es o no posible ese proceso termodinámico para algún valor de .
b) Temperatura de salida si el proceso fuese una simple expansión isoentrópica.
c) Temperatura de salida mínima (límite termodinámico).
d) Temperatura de salida máxima (límite termodinámico).
e) Trabajo específico máximo obtenible.
f) Hacer un esquema de la exergía de la corriente de salida en función de la temperatura de salida.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="Aire":dat:=[T1=(20+273)*K_,p1=200e3*Pa_,T0=(20+273)*K_,T2=(100+273)*K_,T3=(0+273)*K_];

Esquema:

>

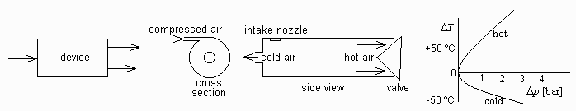
Fig. 1. Esquema del dispositivo, y una aplicación práctica: el tubo refrigerador de Ranque, con un gráfico de prestaciones típicas.

>

Ecs. const.:

>	eqET:=eq1_14;gdat:=get_gas_data(su1):dat:=op(dat),Const,gdat,SI2,SI1:eq5_39a;eq5_39b;eq5_40;eq5_41;eq5_41a;

a) Se desea saber si es posible que, sin necesidad de otras fuentes de energía, se puede conseguir que salgan dos flujos de aire a 100 kPa, uno de fracción másica , a 100 ºC y otro (1- a 0 ºC. Hacer un esquema y justificar mediante las ecuaciones apropiadas si es o no posible ese proceso termodinámico para algún valor de .

La posibilidad de un proceso viene condicionada por el balance exergético (o el entrópico para sistemas aislados). La capacidad de calentar, enfriar o producir trabajo de la corriente de entrada proviene del gradiente de presión con el ambiente (no hay gradiente térmico ni de concentración).

Por unidad de gasto másico de entrada:

>

eqBX:=psi[1]=lambda*psi[2]+(1-lambda)*psi[3]+w[u,out]-Int(1-T0/T,Q)+T0*s[gen];psi:=dh-T0*ds;p2:=p0;p3:=p0;psi[1]:=c[p]*(T1-T0)-T0*(c[p]*ln(T1/T0)-R*ln(p1/p0));psi1_:=subs(dat,evalf(subs(dat,%))):'psi[1]'=evalf(%,2);psi[2]:=c[p]*(T2-T0)-T0*(c[p]*ln(T2/T0)-R*ln(p2/p0));psi2_:=subs(dat,evalf(subs(dat,%))):'psi[2]'=evalf(%,2);psi[3]:=c[p]*(T3-T0)-T0*(c[p]*ln(T3/T0)-R*ln(p3/p0));psi3_:=subs(dat,evalf(subs(dat,%))):'psi[3]'=evalf(%,2);eqBE_:=evalf(psi1_=lambda*psi2_+(1-lambda)*psi3_+w[u,out]-Int(1-T0/T,dQ)+T0*s[gen],2);

i.e.: ¿es posible equilibrar la igualdad 58=9+algo_de_trab_prod+algo_de_calor_atm+algo_de_fricción_interior?

Respuesta. Como todos los términos del segundo miembro son positivos, y ninguno de ellos supera en valor al del primer miembro, se concluye que, para cualquier valor de lambda, existen valores de la degradación de energía en la frontera y/o en el interior, incluso produciendo algo de trabajo, que permiten ajustar el balance exergético. De hecho, una puesta en práctica es el tubo de Ranque esquematizado en la Fig. 1 (Ranque-Hilsch vortex tube, descrito por Ranque en 1933 y estudiado por Hilsch en 1947), que se usa para conseguir refrigeración sin partes móviles ni conexiones eléctricas (aunque el rendimiento frigorífico es muy bajo, del orden del 5%).

Para el tubo de Ranque, al ser el proceso rápido se podrá suponer adiabático, y como no hay trabajo, las ecuaciones quedan:

>

eqBX:='psi[1]=lambda*psi[2]+(1-lambda)*psi[3]+T0*s[gen]';eqBX_:=evalf(psi1_=lambda*psi2_+(1-lambda)*psi3_+T0*s[gen],2);eqBE:='h[1]=lambda*h[2]+(1-lambda)*h[3]';h_href:=c[p]*(T-Tref);eqBE_cp:=T1=lambda*T2+(1-lambda)*T3;lambda_:=subs(dat,solve(%,lambda)):'lambda'=evalf(%,2);eqBX__:=evalf(subs(lambda=lambda_,eqBX_),2);

i.e. sale un 20% del flujo a 100 ºC y un 80% a 0 ºC, con una gran degradación de energía en el interior (un 97% de la exergía).

b) Temperatura de salida si el proceso fuese una simple expansión isoentrópica.

>	T2:=T1*(p2/p1)^((gamma-1)/gamma);T2_:=subs(dat,%):'T2'=evalf(%,2);

c) Temperatura de salida mínima (límite termodinámico).

Será la que se alcanzaría si no hubiese ninguna degradación:

>	T2:='T2':eqBX:='psi[1]=psi[2]';eqBX_:=subs(T2=T2min,%);T2min_:=fsolve(subs(dat,SI0,%),T2min=0..293)*K_:'T2min'=evalf(%,3);

d) Temperatura de salida máxima (límite termodinámico).

Será la que se alcanzaría si no hubiese ninguna degradación:

>	eqBX:='psi[1]=psi[2]';eqBX_:=subs(T2=T2max,%);T2max_:=fsolve(subs(dat,SI0,%),T2max=293..1000)*K_:'T2max'=evalf(%,3);

e) Trabajo específico máximo obtenible.

Será cuando la salida esté en condiciones ambiente (y no hubiese ninguna degradaci\363n):

>	eqBX:='psi[1]=psi[2]+w[u,out]';psi[2]:=c[p]*(T2-T0)-T0*(c[p]*ln(T2/T0)-R*ln(p2/p0));T2=T0;psi2_:=subs(dat,evalf(subs(T2=T0,dat,psi[2]))):'psi[2]'=evalf(%,2);eqBX_:=subs(dat,evalf(subs(dat,psi1_=psi2_+w))):w_:=solve(eqBX_,w):'w[u,out]'=evalf(%,2);

i.e. el trabajo máximo obtenible es la exergía de entrada.

f) Hacer un esquema de la exergía de la corriente de salida en función de la temperatura de salida.

>	'psi[2]'=psi[2];plot([subs(SI0,[[0,w_],[1000,w_]]),subs(T2=T_,dat,SI0,psi[2])],T_=1..500,0..1e5);

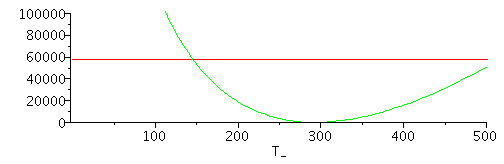i.e. todos los estados de temperatura de salida que queden por debajo de la exergía de entrada, son posibles.

>