>	restart:#"m05_p40"

Para el estudio de un sistema de arranque de un motor diésel marino, a partir de un depósito de aire a 3 MPa, se pide:
a) Calcular la temperatura máxima que se alcanzaría al poner en comunicación el depósito con el cilindro, suponiendo que el volumen inicial cilindro-émbolo no varía y es de 0,1 m3 de aire en condiciones atmosféricas.
b) Calcular el trabajo necesario para acelerar el émbolo, suponiendo que todo el sistema móvil es equivalente a un émbolo libre de 3 toneladas que debe acelerarse en 0,5 s hasta 3 m/s (los efectos gravitatorios no cuentan). Estimar el desplazamiento del émbolo.
c) Calcular el trabajo máximo obtenible del chorro de aire a 3 MPa, y el gasto másico mínimo para la potencia de aceleración antes calculada.
d) Calcular la variación de temperatura interior en un depósito de 1 m3 de aire a 3 MPa al salir 0,2 kg/s de aire durante 10 s.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Aire":dat:=[p9=3e6*Pa_,V1=0.1*m_^3,m[E]=3000*kg_,t=0.5*s_,v=3*m_/s_,V=1*m_^3,mdot=0.2*kg_/s_,Dt=10*s_];

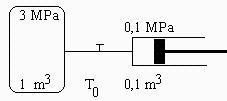
Esquema:

>

>

Eqs. const.:

>	eqET:=subs(eq1_8,eq1_9);eqEE:=eq1_10;gdat:=get_gas_data(su):dat:=op(dat),Const,gdat,SI2,SI1:

a) Calcular la temperatura máxima que se alcanzaría al poner en comunicación el depósito con el cilindro, suponiendo que el volumen inicial cilindro-émbolo no varía y es de 0,1 m3 de aire en condiciones atmosféricas.

El aire del depósito se enfría y el que entra se calienta. Suponiendo depósito infinito y tomando como sistema los 0,1 m3 del cilindro:

>	eqBEcil:=m2*c[v]*T2-m1*c[v]*T1=W12+Q12+h9*(m2-m1);eqBEcil:=(p9-p0)*V1/(gamma-1)=c[p]*T9*(m2-m1);m1:=p0*V1/(R*T0);m1_:=subs(dat,m1):'m1'=evalf(%,2);m2_:=solve(eqBEcil,m2);;m2__:=subs(T9=T0,dat,m2_):'m2'=evalf(%,2);T2:='p2*V1/(m2*R)';T2_:=subs(m2=m2__,p2=p9,dat,T2);

i.e. se calienta más de 100 ºC, pero insuficiente para que se pueda inflamar el combustible, por lo que el motor ha de aspirar y comprimir aire atmoséfrico para que su temperatura alcance los 1000 K y al introducir el combustible se inflame.

b) Calcular el trabajo necesario para acelerar el émbolo, suponiendo que todo el sistema móvil es equivalente a un émbolo libre de 3 toneladas que debe acelerarse en 0,5 s hasta 3 m/s (los efectos gravitatorios no cuentan). Estimar el desplazamiento del émbolo.

Si no hay fricción, el trabajo se invertirá en la energía cinética, y para el desplazamiento supondremos aceleración constante (equivaldría a presión constante):

>	P:=(1/2)*m[E]*v^2/t;P_:=subs(dat,P);a:=v/t;a_:=subs(dat,a);a[max]:=(p9-p0)*A/m[E];a_[max]:=subs(A=Pi*(0.5*m_)^2/4,dat,a[max]);

Nota: se ha comprobado que la aceleración dada es conseguible en un caso real de un émbolo de medio metro de diámetro.

c) Calcular el trabajo máximo obtenible del chorro de aire a 3 MPa, y el gasto másico mínimo para la potencia de aceleración antes calculada.

>	w[max]:=Dh-T0*Ds;w[max]:=c[p]*(T9-T0)-T0*(c[p]*ln(T9/T0)-R*ln(p9/p0));w_[max]:=subs(dat,evalf(subs(T9=T0,dat,w[max]))):'w[max]'=evalf(%,2);mdot_min:='P/w[max]';mdot_min_:=subs(dat,P_/w_[max]);

d) Calcular la variación de temperatura interior en un depósito de 1 m3 de aire a 3 MPa al salir 0,2 kg/s de aire durante 10 s.

Expansión isoentrópica: p*m^-gamma=cte

>	m9:=p9*V/(R*T0);m9_:=subs(dat,m9);Dm:=mdot*Dt;Dm_:=subs(dat,Dm);p8:='p9*((m9-Dm)/m9)^gamma';p8_:=subs(dat,p8):'p8'=evalf(%,2);T8:='p8*V/((m9-Dm)*R)';T8_:=subs(dat,T8);

i.e. se enfría algo más de 6 C.

>