>	restart:#"m05_p12"

Se desea analizar la energía requerida para hacer pasar una corriente de agua a presión ambiente desde 10 °C hasta 120 °C. Se pide:

a) Trabajo mínimo necesario disponiendo libremente de la atmósfera.

b) Energía necesaria si se utiliza un calentador eléctrico.

c) Energía necesaria si se utiliza un calentador a gas de rendimiento energético 0,8. ¿Por qué son de uso más corriente (p.e. para agua sanitaria) los calentadores a gas que los eléctricos?

d) Trabajo mínimo necesario disponiendo de una única máquina de Carnot (temperaturas de funcionamiento fijas).

e) Trabajo mínimo necesario disponiendo de dos máquinas de Carnot.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":dat:=[T1=(10+273)*K_,T2=(120+273)*K_,eta[cal]=0.8];

Esquema:

>

>

Eqs. const.:

>	eqET:=eq1_15;eqEE:=eq1_17;ldat:=get_liq_data(su):pv_dat:=get_pv_data(su):gdat:=get_gas_data(su):dat:=op(dat),Const,gdat,ldat,SI2,SI1:

a) Trabajo mínimo necesario disponiendo libremente de la atmósfera.

Se supone p=p0=100 kPa y T0=T1. Cambio de fase a 100 ºC.

>	wmin:=h12-T0*s12;T100_:=solve(subs(Const,p0)=pv(T),T);h12_:=c*(T100-T1)+h[lv0]+c[p]*(T2-T100);s12_:=c*ln(T100/T1)+h[lv0]/T100+c[p]*ln(T2/T100);wmin_:=subs(SI1,evalf(subs(T100=T100_,dat,subs(dat,h12_-T0*s12_)))):'wmin'=evalf(%/(1000*J_/kJ_));

b) Energía necesaria si se utiliza un calentador eléctrico.

>	eqBE;wele:=h12;wele_:=subs(SI1,evalf(subs(T100=T100_,dat,subs(dat,h12_)))):'wele'=evalf(%/(1000*J_/kJ_));

c) Energía necesaria si se utiliza un calentador a gas de rendimiento energético 0,8. ¿Por qué son de uso más corriente (p.e. para agua sanitaria) los calentadores a gas que los eléctricos?

>	qgas:=h12/eta[cal];qgas_:=subs(SI1,wele_/subs(dat,eta[cal])):'qgas'=evalf(%/(1000*J_/kJ_));

Por una parte, el coste energético del gas es 2 ó 3 veces inferior al de la electricidad, y por otra la potencia eléctrica instalada también es 2 ó 3 veces menor;

d) Trabajo mínimo necesario disponiendo de una única máquina de Carnot (temperaturas de funcionamiento fijas).

>	Q1:=h12;eq1:=eta[Carnot]=1-T1/T2;eq2:=eta[Carnot]=1-Q2/'Q1';eq3:=rhs(eq1)=subs(Q2=Q1-w[Carnot],rhs(eq2));w[Carnot_]:=solve(eq3,w[Carnot]);w[Carnot__]:=subs(h12=wele_,dat,w[Carnot_]):'w[Carnot]'=evalf(%/(1000*J_/kJ_),2);

d) ) Trabajo mínimo necesario disponiendo de dos máquinas de Carnot.

Caso Ti<T100

>	eta_maq1:=(Ti-T1)/Ti;wmaq1:=c*(Ti-T1)*eta_maq1;eta_maq2:=(T2-T1)/T2;wmaq2:=(h12-c*(Ti-T1))*eta_maq2;wcaso1:=proc(T) global Ti,dat; RETURN(subs(Ti=T,h12=wele_,dat,wmaq1+wmaq2)) end;pl1:=subs(dat,SI0,[seq([T1+10*K_*i,wcaso1(T1+10*K_*i)],i=0..9)]):

Caso Ti>T100

>	eta_maq1:=(Ti-T1)/Ti;wmaq1:=(c*(Ti-T1)+h[lv0]+c[p]*(Ti-T100))*eta_maq1;eta_maq2:=(T2-T1)/T2;wmaq2:=c[p]*(T2-Ti)*eta_maq2;wcaso2:=proc(T) global Ti,dat; RETURN(subs(ldat,subs(Ti=T,dat,wmaq1+wmaq2))) end;pl2:=subs(T100=T100_,dat,SI0,[seq([T100+10*K_*i,wcaso2(T100+10*K_*i)],i=0..2)]);

>	plot([[[373,600000],[373,subs(SI0,w[Carnot__])]],pl1,pl2],T=283..393,w=600000..subs(SI0,w[Carnot__]),color=black);

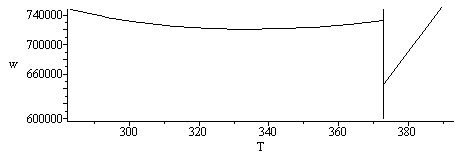i.e. la primera bomba calentando el agua hasta 100 °C y vaporizándola, la segunda sólo calentando el vapor (nótese que el mínimo local es w=720 kJ/kg).

>