>	restart:#"m04_p47"

Un depósito rígido de 100 litros contiene metano, inicialmente a 0,9 MPa y -110 ºC, y se deja atemperar en un ambiente a 90 kPa y 15 ºC. Se pide:

a) Masa de gas encerrada.

b) Presión final.

c) Calor intercambiado.

d) Entropía generada en el proceso.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(T1>0,T2>0):

>	su:="CH4":dat:=[V=0.1*m_^3,p1=0.9e6*Pa_,T1=(-110+273)*K_,p0=90e3*Pa_,T0=(15+273)*K_];

>	dat:=[op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1]:get_pv_data(su):T[cr]=subs(dat,T[cr]);p[cr]=subs(dat,p[cr]);R=subs(dat,R);

a) Masa de gas encerrada.

La presión inicial es tan grande, y la temperatura tan baja, que habría que comprobar que es gas, y luego usar el MEC, porque las correcciones por compresibilidad respecto al MGI serán grandes.

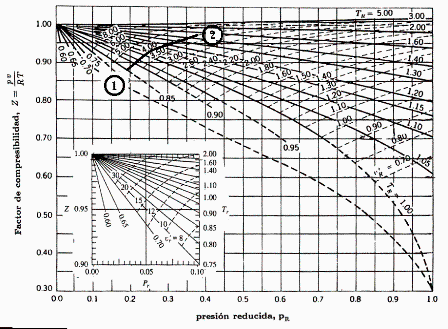
>	pvT1_:=subs(dat,evalf(subs(dat,pv(T1))));pR=p/p[cr];TR=T/T[cr];pR1:=subs(dat,p1/p[cr]);TR1:=subs(dat,T1/T[cr]);Z1_:=0.87;mM:=p1*V/(Z1*R*T1);mM_:=subs(dat,subs(Z1=Z1_,dat,%));

Efectivamente estaba en estado gaseoso, pues a esa temperatura no licúa hasta 1,8 MPa. Mirando en el gráfico Z-pR se obtiene Z1=0,87, y por tanto la masa es de 1,22 kg (el MGI hubiera dado sólo 1,06 kg).

b) Presión final.

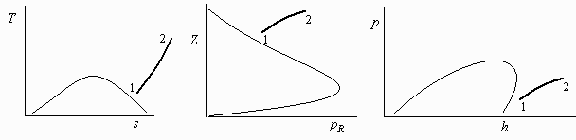
El proceso es a V=cte.; una ecuación con una incógnita, p2, pero con una función gráfica Z2(p2,T2), que puede resolverse por aproximaciones sucesivas, o con ayuda de las curvas de volumen pseudo-crítico constante, que vienen dibujadas en algunos diagramas Z-pR.

Método excñusivamente gráfico: se calcula el volumen pseudo-crítico inicial, y se sigue esa curva hasta llegar a la isoterma final (Fig. 1):

>	vR=v/v[cr];vR=v/(Z[cr]*R*T[cr]/p[cr]);vRs=v/v[cr,id];vRs=v/(R*T[cr]/p[cr]);vRs:=subs(dat,subs(m=mM_,dat,(V/m)/(R*T[cr]/p[cr])));pR2:=0.4;p2_:=subs(dat,pR2*p[cr]);

	(1)

i.e. la curva de vRs=0,4 (la precisión no es grande) corta a la de TR=1,5 en pR=0,4, a la quer corresponde una presión final de 1,9 MPa.

Ahora repetimos el cálculo sin ayuda de las isocoras pseudo-críticas. Se trata de resolver una ecuación, v1=v2, con una incógnita, p2, pero con una función gráfica Z2(p2)..

>	eq12:=Z2*R*T2/p2=V/m;p2_MGI:=p1*T2/T1;TR2:=subs(dat,T0/T[cr]);p2_MGI_:=subs(T2=T0,dat,p2_MGI);p2_:=%;pR2:=subs(dat,subs(dat,p2_/p[cr]));Z2_:=0.98;eq12_:=subs(dat,subs(Z2=Z2_,T2=T0,p2=p2_,m=mM_,dat,eq12));

>	p2_:=2.0e6*Pa_;pR2:=subs(dat,subs(dat,p2_/p[cr]));Z2_:=0.96;eq12_:=subs(dat,subs(Z2=Z2_,T2=T0,p2=p2_,m=mM_,dat,eq12));

>	p2_:=1.8e6*Pa_;pR2:=subs(dat,subs(dat,p2_/p[cr]));Z2_:=0.97;eq12_:=subs(dat,subs(Z2=Z2_,T2=T0,p2=p2_,m=mM_,dat,eq12));

	(2)

que se puede ya dar por buena, i.e. al atemperarse queda a 1,8 MPa.

c) Calor intercambiado.

Se va a tomar un valor constante de cp, e.g. el valor en condiciones normales, pues las variaciones de cp con T y p son pequeñas.

>

eqBE:=DE=Q+W;W=0;Q:=DH-D(pV);Q:=m*Dh-(p2-p1)*V;Dh:=Dhid-Dhcc2+Dhcc1;Dhid:=c[p]*(T2-T1);c[p]=subs(dat,c[p]);Dhid:=subs(T2=T0,dat,Dhid);Dhcc1_RTcr:=0.37;Dhcc1:=subs(dat,Dhcc1_RTcr*R*T[cr]);Dhcc2_RTcr:=0.1;Dhcc2:=subs(dat,Dhcc2_RTcr*R*T[cr]);Dh_:=Dh;DpV=(p2-p1)*V;DpV_:=subs(SI2,dat,subs(dat,(p2_-p1)*V));Q_:=subs(dat,subs(dat,SI2,mM_*Dh_-DpV_));

	(3)

i.e. el metano recibe 280 kJ al atemperarse.

d) Entropía generada en el proceso.

Será igual al incremento de entropía del universo compuesto por el metano más el ambiente; no se contabiliza aquí la del recipiente, aunque sería bastante mayor, debido a la relación de masas.

>

Sgen:='m*Ds-Q/T0';Sgen:='m*(Dsid-Dscc2+Dscc1)-Q/T0';Dsid:=Int(cp/T,T=T1..T2)-R*ln(p2/p1);Dsid:=subs(dat,simplify(subs(cp=c[p],T2=T0,p2=p2_,dat,SI2,value(%))));'pR1'=pR1;'TR1'=TR1;Dscc1_R:=0.33;Dscc1:=subs(dat,Dscc1_R*R);Dscc2_R:=0.1;Dscc2:=subs(dat,Dscc2_R*R);DS='mM*(Dsid-Dscc2+Dscc1)';DS_:=subs(dat,subs(dat,mM_*(Dsid-Dscc2+Dscc1)));Q_T0='Q/T0';Q_T0_:=subs(dat,subs(dat,Q_/T0));Sgen_:=DS_-Q_T0_;

	(4)

i.e., unos 260 J/K.

Para que pueda servir de comparación, los valores más precisos (datos NIST) son: m=1,208 kg (rho=12,08 kg/m3), p2=1,734 MPa, Q=247 kJ, DS=1130 J/K, Sgen=272 J/K, cp(163 K; 0 Pa)=2077 J/(kg·K), cp(163 K; 0,9 MPa)=2475 J/(kg·K), cp(288 K; 0 Pa)=2203 J/(kg·K), cp(288 K; 1,734 MPa)=2321 J/(kg·K). La discrepancia por haber tomado como valor medio de cp(T,0)=2180 J/(kg·K) es algo mayor del 10% en el valor del calor, y de un 4% en la Sgen.