>	restart:#"m04_46"

Se quiere usar el siguiente modelo termodinámico:

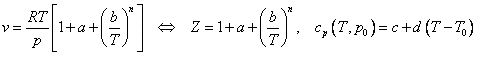
con a=2.41•10-3 m3/kg, b=22.1 m3/(kg•K), n=1.6, c=638 J/(kg•K), d=0.43 J/(kg•K2), p0=100 kPa y T0=298 K, para modelizar el comportamiento del SO2 en el siguiente problema. Dentro de un cilindro vertical de 0,3 m de diámetro, un émbolo de 45 kg separa dos volúmenes iguales, el superior contiene aire a 105 kPa, y el inferior 0,1 kg de SO2. Inicialmente, todo está a 25 ºC. Entonces, se pone en contacto la base inferior con una fuente térmica a 600 K. Suponiendo que todas las demás superficies (incluyendo las del pistón) son adiabáticas, se pide:

a) Volumen de SO2 inicial.

b) Masa de aire atrapado.

c) Temperatura del aire en el nuevo equilibrio.

d) Trabajo recibido por el aire atrapado.

e) Calor recibido por el SO2.

f) Generación de entropía en el proceso.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):assume(p0>0,p1>0,p2>0,T>0,T0>0,T1>0,T2>0,TR>0):

>	su1:="SO2":su2:="Aire":EOS:=v=R*T/p*(1+a+(b/T)^n);cpS:=c[p,T,p0]=c+d*(T-T0);dat:=[a=2.41e-3,b=22.1*K_,n=1.6,c=638*J_/(kg_*K_),d=0.43*J_/(kg_*K_^2),p0=1e5*Pa_,T0=298*K_,D=0.3*m_,mE=45*kg_,VA1=VS1,pA1=105e3*Pa_,mS=0.1*kg_,TR=600*K_];

Esquema:

>

Eqs. const.:

>	Sdat_MSP:=get_gas_data(su1),get_liq_data(su1):Adat:=get_gas_data(su2):dat:=op(dat),Const,SI2,SI1:#Cuidado; comflicto del c del Sdat con el c del dat.

a) Volumen de SO2 inicial

Lo primero es tener una idea del estado de agregación del SO2, aunque presumiblemente estará gaseoso, por el tipo de ecuación de estado propuesta.

>	T[b]=subs(Sdat_MSP,T[b]);eqBF:=pS1=pA1+mE*g/A;eqA:=A=Pi*D^2/4;eqA_:=evalf(subs(dat,%));eqBF_:=subs(eqA_,dat,eqBF);eqVS1_MGI:=VS1=mS*RS*T0/pS1;eqVS1_MGI_:=subs(RS=R,eqBF_,Sdat_MSP,dat,%);eqVS1:=VS1=mS*rhs(EOS);eqVS1_:=subs(Sdat_MSP,p=pS1,eqBF_,T=T0,dat,%);Vtotal_:=2*rhs(%);VA1:=VS1;

Efectivamente, a 100 kPa el SO2 es gas por encima de -10 ºC, así que a 105 kPa será gas. Debido al peso del émbolo, el CO2 está a 111 kPa (6 kPa más que el aire).Con el modelo de gas ideal, deduciríamos que el SO2 ocupa 34,9 litros, pero con el modelo del enunciado deducimos que ocupa 35,4 L.

b) Masa de aire atrapado

>	eqmA:=mA=pA1*VA1/(RA*T0);eqmA_:=subs(RA=R,Adat,eqVS1_,dat,%);

	(1)

i.e. hay 43,5 g de aire atrapado.

c) Temperatura del aire en el nuevo equilibrio

>

eq1:=mS*vS2+mA*vA2=Vtotal;eq2:=pS2=pA2+mE*g/A;eq3:=TA2=TA1*(pA2/pA1)^((gamma-1)/gamma);eq123:=subs(vS2=rhs(EOS),R=RS,T=TR,p=pS2,eq2,vA2=RA*TA2/pA2,eq3,eq1);eq123_:=subs(eqmA_,RA=R,Adat,TA1=T0,Vtotal=Vtotal_,RS=R,Sdat_MSP,eqA_,dat,SI0,%);pA2_:=fsolve(%,pA2=1e5..2e5)*Pa_;plot(lhs(eq123_)-rhs(eq123_),pA2=1e5..3e5);TA2_:=subs(pA2=pA2_,TA1=T0,Adat,dat,rhs(eq3));VA2_:=subs(eqmA_,Adat,dat,mA*R*TA2_/pA2_);pS2_:=pA2_+subs(eqA_,dat,mE*g/A);

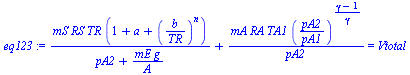	(2)

i.e. el aire queda ocupando 25 litros a 168 kPa y 340 K, y el SO2 ocupando 45 litros a 173 kPa y los 600 K de la fuente.

d) Trabajo recibido por el aire atrapado

Como el proceso que sufre el aire es isoentrópico,

>	eqW:=W=-Int(p,V);eqW:=W=-Int(pA1*(VA1/V)^gamma,V=VA1..VA2);eqW_:=value(%);eqW__:=subs(VA2=VA2_,eqVS1_,Adat,dat,%);

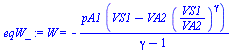	(3)

i.e. el aire recibe 1300 J de trabajo.

e) Calor recibido por el SO2

>	eqBE:=DE=W+Q;QS:=DES-WS;WS:=-WA-mE*g*Dz;WS:=-WA-mE*g*(VS2-VS1)/A;WS_:=subs(WA=rhs(eqW__),eqA_,eqVS1_,VS2=Vtotal_-VA2_,dat,%);DE_MGP:=mS*cv*DT;DE_MGP:=mS*(c[p]-R)*(TS2-TS1);DE_MGP_:=subs(Sdat_MSP,TS2=TR,TS1=T0,dat,%);QS_MGP_:=DE_MGP_-WS_;

	(4)

i.e. el SO2 realiza un trabajo de 1400 J y, con el MGP, acumula una energía interna de 14400 J recibiendo un calor de 15800 J de la fuente.

Para calcular estos últimos valores con el modelo dado, conviene trabajar con entalpías y luego sustituir en DE=DH-D(pV).

Además, a la vista del dato de cp(T,p0), hay que elegir el camino de integración de la Fig. 1.

>

DE:=DH-'D(p*V)';DE:=m*Dh-'D(p*V)';eqdh:=dh=c[p]*dT+(1-alpha*T)*v*dp;eqDh:=Dh=Int(c[p],T)+Int((1-alpha*T)*v,p);eqDh:=Dh=Int(c[p],T)+Int(v,p)-Int(T*alpha*v,p);EOS;Tav:=T*simplify(diff(rhs(EOS),T));v_Tav:=simplify(rhs(EOS)-Tav);eqDh:=Dh=Int(c[p],T)+Int(v_Tav,p);eqDh:=h2-h1=Int(c[p,T,p0],T=T1..T2)+Int(subs(T=T2,v_Tav),p=p0..p2)-Int(subs(T=T1,v_Tav),p=p0..p1);eqDh_:=value(eval(subs(cpS,%)));eqDh12_:=evalf(subs(dat,T2=TR,T1=T0,p2=pS2_,p1=pS1,eqBF_,Sdat_MSP,dat,SI0,eqDh_));DE_:=subs(eqBF_,VS2=Vtotal_-VA2_,eqVS1_,dat,mS*rhs(eqDh12_)*(J_/kg_)-(pS2_*VS2-pS1*VS1));Q_:=DE_-WS_;

	(5)

i.e., con el modelo del enunciado, el SO2 almacena 17,3 kJ recibiendo un calor de 18,7 kJ. Vemos que es un 20% mayor que el del MGP.

f) Generación de entropía en el proceso.

Como la evolución del aire es isoentrópica y el émbolo se supone que no roza, sólo se generará entropía en la transmisión de calor con salto térmico.

>

Sgen:=Sum(DS,i);Sgen:=DSR+DSS;Sgen:=QR/TR+mS*Ds;Sgen:=-Q/TR+mS*(Int(c[p]/T,T)-Int(alpha*v,p));Sgen:=-Q/TR+mS*(Int(rhs(cpS)/T,T)-Int(Tav/T,p));Sgen:=-Q/TR+mS*(Ds_0+Ds_2-Ds_1);Ds_0:=int(rhs(cpS)/T,T=T0..TR);Ds_2:=int(subs(T=T2,Tav/T),p=p0..p2);Ds_1:=int(subs(T=T1,Tav/T),p=p0..p1);Ds_0_:=evalf(subs(dat,SI0,Ds_0))*J_/(kg_*K_);Ds_2_:=evalf(subs(T2=TR,dat,Sdat_MSP,p2=pS2_,SI0,Ds_2))*J_/(kg_*K_);Ds_1_:=evalf(subs(dat,Sdat_MSP,p1=pS1,eqBF,eqA_,T1=T0,dat,SI0,Ds_1))*J_/(kg_*K_);Sgen_:=subs(dat,[-Q_/TR,mS*(Ds_0_+Ds_2_-Ds_1_)]);Sgen_:=convert(%,`+`);Sgen_MGP:=-Q/TR+mS*(c[p]*ln(TR/T0)-R*ln(pS2/pS1));Sgen_MGP_:=subs(dat,evalf(subs(Sdat_MSP,Q=Q_,pS2=pS2_,eqBF_,dat,%)));

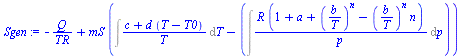	(6)

i.e. la generación de entropía ha sido de 23 J/K, bastante mayor de la que nos daría el modelo de gas perfecto: 5 J/K).

>