>	restart:#"m04_p43"

En un depósito rígido de 1 m3 hay vapor de agua, inicialmente a 400 ºC y 10 MPa, que se está enfriando. Se pide
a) Masa de vapor encerrada.
b) Temperatura a la que empezará a condensar agua.
c) Calor desprendido entre los dos instantes mencionados.
d) Estado final a 20 ºC

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":dat:=[V=1*m_^3,T1=(400+273)*K_,p1=10e6*Pa_,T3=(20+273)*K_];

Eqs. const.:

>	dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):

a) Masa de vapor encerrada.

Suponiendo válido el modelo de gas ideal por la alta temperatura (aunque la presión es alta y habría que ver si las correciones por compresibilidad son importantes. No hay posibilidad de que estuviese en fase líquida porque está a T>Tcr=374 ºC.

>	eqM_MGI:=m=p1*V/(R*T1);eqM_MGI_:=subs(dat,%);

i.e., hay unos 32 kg de vapor dentro (37,8 kg con los datos más precisos del NIST).

b) Temperatura a la que empezará a condensar agua.

La evolución es a volumen constante, y el estado 2 será cuando se verifique la ecuación de Clapeyron (o la de Antoine). Si seguimos con el MGI para el vapor:

>	eq12:=V2-V1=0;eq12:=m*R*T2/p2-m*R*T1/p1=0;p2:=pv(T2);T2_:=solve(subs(dat,eq12),T2);p2_:=subs(dat,evalf(pv(T2_)));

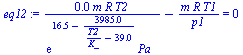i.e., empezará a condensar a 570 K (cuando la presión sea de 8,5 MPa). Recuérdese que al ser a V=cte, la condensación continuaría al ir bajando la temperatura (las sustancias puras cambian de fase a temperatura constante sólo si la presión se mantiene constante). Con los datos del NIST, sería a 561 K y 7,22 MPa, siendo la variación debida a la discrepancia en la densidad inicial.

c) Calor desprendido entre los dos instantes mencionados.

Con el modelo de gas perfecto:

>	eqBE:=DE=Q+W;eqBE:=Q=m*c[v]*(T2-T1);eqBE_:=subs(eqM_MGI,T2=T2_,dat,eqBE);c[v]=subs(dat,c[v]);

i.e., salen 4,7 MJ de calor (9,59 MJ con los datos del NIST). Nótese que si se hubiese usado un mejor valor medio para el cv del vapor (en vez del valor a 15 ºC), la discrepancia no hubiera sido tan grande (a 400 ºC y 10 MPa es cv=2250 J/(kg·K), en vez del valor usado, 1440).

d) Estado final a 20 ºC

>	T3=subs(dat,T3);pvT3_:=subs(dat,evalf(subs(dat,pv(T3))));eqx:=v=(1-x)*vliq+x*vvap;eqx:='V/m=(1-x)/rho+x*R*T3/p3';x_:=subs(eqM_MGI_,p3=pvT3_,dat,solve(%,x));

i.e. en el estado final a 20 ºC, la presión interior será de 2,3 kPa, y la fracción másica de vapor del 0,05% (prácticamente toda la masa ha condensado, ocupando 32 litros los 32 kg, con 32*0.0005=16 g de vapor ocupando los 968 litros restantes).

>