>	restart:#"m04_p42"

Dentro de un recipiente de 1 m3 hay 30 kg de un fluido de masa molar 0,042 kg/mol, en equilibrio líquido-vapor a 460 kPa y 270 K, Sabiendo que tiene el punto crítico a 360 K y 4,6 MPa, se pide:
a) Fracciones másica y volumétrica de vapor.
b) Calor necesario para vaporizar la parte líquida a presión constante.
c) ¿Qué pasaría si se calienta a volumen constante?

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	dat:=[V=1*m_^3,mt=30*kg_,M=0.042*kg_/mol_,p=460e3*Pa_,T=270*K_,Tcr=360*K_,pcr=4.6e6*Pa_];

>	dat:=op(dat),Const,SI2,SI1:

a) Fracciones másica y volumétrica de vapor.

Se puede resolver de varias maneras.

Aproximación A: suponer que casi no hay líquido (si fuese agua, 30 kg ocuparían sólo un 3% del volumen (30 L de 1000 L)

>	eqR:=R=R[u]/M;eqR_:=subs(dat,%);mvapMGIt:=p*V/(R*T);mvapMGIt_:=subs(eqR_,dat,%);mliq:='mt-mvapMGIt';mliq_:=subs(eqR_,dat,%);

y ahora se podría iterar restando el volumen que ocupa el líquido.

Aproximación B: suponer que casi toda la masa es líquida (si fuese un vapor de la densidad del aire, todo lleno sólo contendría 1, 2 kg de gas). Con la densidad del líquido obtendríamos el volumen que ocupa y, por diferencia, el volumen de vapor, cuya masa calcularíamos con el modelo de gas ideal. En este caso, al no disponer de la densidad del líquido, este método no es bueno.

>

Aproximación C: usamos el método de estados correspondientes. Éste es el camino más preciso.

>	eqpR:=pR=subs(dat,p/pcr);eqTR:=TR=evalf(subs(dat,T/Tcr));eqZ:=Z=p*V/(m*R*T);eqZ_:=subs(m=mt,R=R[u]/M,dat,subs(dat,eqZ));Zvap:=0.90;Zliq:=0.02;

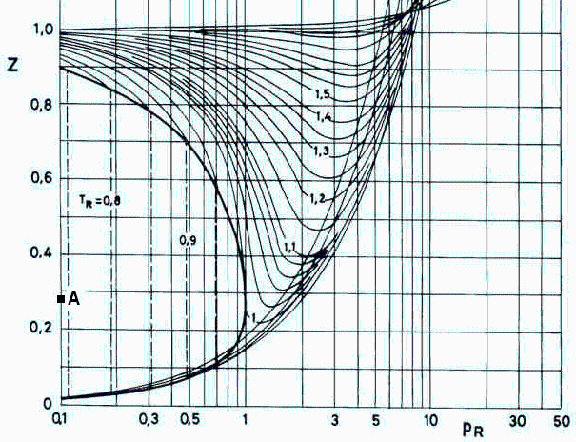
A la luz de los datos, se trata del estado A (Fig. 1), de donde se deducen los volúmenes y cantidades de sustancia en cada fase:

>

m_vap:='p*Vvap/(Zvap*R*T)';m_liq:='p*Vliq/(Zliq*R*T)';eqV:=V=Vvap+Vliq;eqm:=mt='m_vap+m_liq';sol_V:=subs(eqR_,dat,subs(dat,solve({eqV,eqm},{Vvap,Vliq})));m_vap_:=subs(eqR_,dat,subs(sol_V,dat,m_vap));m_liq_:=subs(eqR_,dat,subs(sol_V,dat,m_liq));eqphi:=phi=Vvap/V;eqphi_:=subs(sol_V,dat,%);eqx:=x=mvap/mt;eqx_:=subs(mvap=m_vap_,dat,%);

i.e. el vapor ocupa el 95% del volumen, y su fracción másica es del 30%. Nótese que Z=(1-x)*Zliq+x*Zvap, como se puede deducir de V/m=(Vliq+Vvap)/(mliq+mvap)=xliq*vliq+xvap*vvap.

b) Calor necesario para vaporizar la parte líquida a presión constante.

Será Q=mliq*hlv, pero como no sabemos la entalpía de cambio de fase, nos vemos obligados a usar el método de estados correspondientes (del diagrama de correcciones de entalpía por compresibilidad, se deduce hlv).

>	Q:=m_liq*hlv;hlv:=Dhcc_liq-Dhcc_vap;

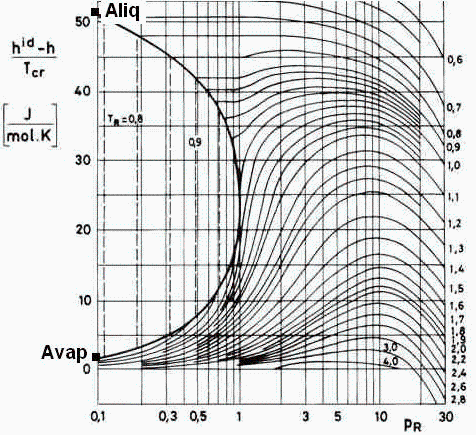
Del gráfico se obtiene Avap=2 J/(mol·K) y Aliq=51 J/(mol·K).

>	Dhcc_vap:=Avap*Tcr/M;Avap:=2*J_/(mol_*K_);Dhcc_vap_:=subs(dat,Dhcc_vap);Dhcc_liq:=Aliq*Tcr/M;Aliq:=51*J_/(mol_*K_);Dhcc_liq_:=subs(dat,Dhcc_liq);hlv_:=Dhcc_liq_-Dhcc_vap_;Q_:=m_liq_*hlv_;

i.e., su entalpía de vaporización en esas condiciones es de 420 kJ/kg, y hay que aportar 8,8 MJ para vaporizar todo el líquido a presión constante (e.g. en un dispositivo cilindro-émbolo).

c) ¿Qué pasaría si se calienta a volumen constante?

Que iría aumentando la temperatura, pero sobre todo la presión, y podría romperse (catastróficamente) el recipiente.

Se podría ir calculando la evolución con el método de estados correspondientes, pero es complicado porque para cada estado habría que resolver gráficamente la ecuación V=Z(p,T)mRT/p=cte. Si lo hacemos en función de la temperatura, iríamos eligiendo valores de T, y la p vendría dada por el equilibrio bifásico (que se vería en el diagrama Z-pR); el nivel de líquido se calcularía con la Zs, de Z=pV/(mRT), y Zvap y Zliq como antes. Cuando ya no quedase más que una fase (presumiblemente desapareciendo todo el líquido), data la T, la p se calcularía iterando en V=Z(p,T)mRT/p=cte.

>