>	restart:#"m04_p40"

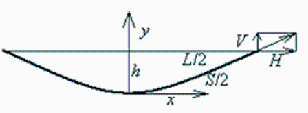
Se desea saber cuánto desciende el punto medio de un cable colgante entre apoyos separados 500 m, debido a la dilatación desde el invierno al verano, en función de la flecha en invierno, z0, y el valor numérico para z0=5 m y T=30 ºC.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(L>0,DT>0,a>0,x1>0):

>	su:="Acero":dat:=[L=500*m_,h=5*m_,DT=30*K_,alpha=12e-6/K_];

Esquema:

>

>

Eqs. const.:

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:

Sabemos que, con las aproximaciones usuales de cables colgantes (flexibles, inextensibles (no elásticos), de masa por unidad de longitud constante, y sometidos a la única carga del peso), éstos adoptan la forma de equilibrio llamada catenaria (parece ser que fue Huygens el primero en descubrirlo, pues hasta Galileo suponía que la forma sería de parábola).

Sea:

L=longitud entre apoyos

S=longitud de la cadena

h=z0=flecha

Se trata de obtener la función S(L,h), dilatarla S_=S*(1+alpha*DT), e invertirla para obtener el nuevo valor h_(S_,L). Pero el desarrollo no es sencillo.

Catenaria exacta.

>

y:=a*(cosh(x/a)-1);eqDat:=h=subs(x=L/2,y);a_:=fsolve(subs(dat,SI0,%),a)*m_;ydim_:=subs(a=a_,dat,SI0,y);S:=Int(sqrt(1+Diff('y',x)^2),x=0..L/2);S:=simplify(convert(value(%),trig));S:=a*sinh((L/2)/a);S_:=evalf(subs(a=a_,dat,%));DS_:=S_-subs(dat,L/2);S__:=subs(dat,S_*(1+alpha*DT));DS__:=S__-subs(dat,L/2);a__:=fsolve(subs(dat,SI0,S=S__),a=1e3..1e5)*m_;ydim_dil:=subs(a=a__,dat,SI0,y);h_:=evalf(subs(a=a__,dat,SI0,rhs(eqDat)))*m_;

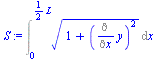i.e., el punto mínimo baja de 5 m a 7,7 m, una cantidad relativamente importante.

Para tener una expresión algebraica donde se viera la dependencia funcional y no sólo el valor numérico, podríamos haber usado una aproximación polinómica sencilla, una simple parábola y=ax2, y es de suponer que daría lo mismo.

>

y:=a*x^2;eqDat:=h=subs(x=L/2,y);a_:=fsolve(subs(dat,SI0,%),a)*m_;S:=Int(sqrt(1+Diff('y',x)^2),x=0..L/2);S:=simplify(convert(value(%),trig));S:=convert(series(%,a=0,4),polynom);S_:=evalf(subs(a=a_,dat,SI0,%))*m_;DS_:=S_-subs(dat,L/2);S__:=subs(dat,S_*(1+alpha*DT));DS__:=S__-subs(dat,L/2);a__:=fsolve(subs(dat,SI0,S=S__),a=0..1)*m_;h_:=evalf(subs(a=a__,dat,SI0,rhs(eqDat)))*m_;

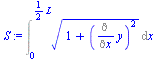Efectivamente, da lo mismo, pero tampoco se ha llegado a una solución analítica.

. Incluso se podría aproximar la catenaria por un triángulo, suponiendo concentrado todo el peso en el punto medio.

Sea y=Dz0/z0 el desplazamiento relativo del punto más bajo.

>

y:=sqrt((1/(4*epsilon2^2)+1)*(1+epsilon1)^2-1/(4*epsilon2^2))-1;eqe1:=epsilon1=alpha*DT;subs(dat,eqe1);eqe2:=epsilon2=h/L;evalf(subs(dat,eqe2));y11:=convert(series(y,epsilon1=0,2),polynom);y11_:=subs(eqe1,eqe2,dat,y11);h_:=(1+y11)*h;h_:=subs(y11=y11_,dat,%);h__:=(1+'y')*h;h__:=subs(eqe1,eqe2,dat,%);

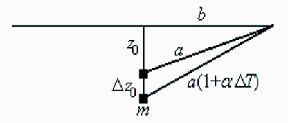
Representación gráfica relativa (no a escala).

>	plot([[[0,-h_/m_],[250,0]],[[0,-h__/m_],[250,0]],ydim_-5,ydim_dil-7.67],x=0..250,thickness=1,color=black);#,scaling=constrained

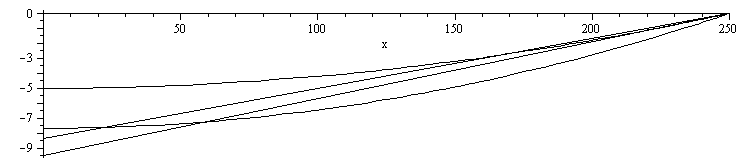¡Vaya!, parece que este modelo lineal (y11) en alpha*DT no es muy bueno, pues bajaría de 5 m a 9,5 m, en vez de a 7,7 m como da la solución exacta y la aproximación parabólica. Y ni siquiera el triangular exacto, que bajaría de 5 m a 8,4 m.

Por cierto, ¿cómo puede haber tanta diferencia entre el lineal y el exacto, si se trata de un desarrollo en serie con alpha*DT=0.00036?

Si retenemos más términos en el desarrollo en serie, tenemos:

>	'y'=y;'y11'=y11;for i from 2 to 10 do cat(y1,i):=convert(series(y,epsilon1=0,i),polynom);print(i-1,subs(eqe1,eqe2,dat,%));end do:

¡Vaya!, el desarrollo es divergente. Y si desarrollamos en función de h/L:

>	y21:=convert(series(y,epsilon2=0,2),polynom);y21_:=subs(eqe1,eqe2,dat,y21);for i from 0 to 10 do convert(series(y,epsilon2=0,i),polynom);print(i-1,subs(eqe1,eqe2,dat,%));end do:plot3d(y,epsilon1=0..4e-4,epsilon2=0..4e-4,axes=boxed);

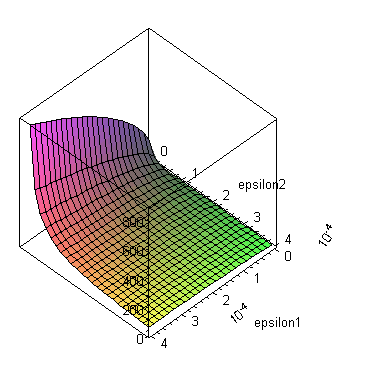Claro, es que, aunque epsilon1<epsilon2, la función y es singular en epsilon2=0, y lo que influye no es epsilon2 sino epsilon2^2.

La explicación es que el desarrollo en series de epsilon1 es inestable para valores pequeños de epsilon2, que es nuestro caso.

>

ADICIONAL

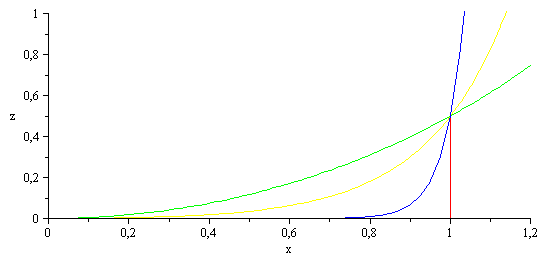
Puede comprobarse que no todos los cosh(x) son catenarias, pues sólo es si se verifica que la variación de fuerza vertical dV=d(H*dz/dx) es igual al peso del arco wds=w*sqrt(1+zp^2)dx.. Elijo L=2, h=0.5, por ejemplo.

>	eqTrial:=z=a*(cosh(b*x)-1);eqDat:=h=subs(eqTrial,x=L/2,z);z_:=subs(eqTrial,a=solve(eqDat,a),z);plot([[[1,0],[1,0.5]],subs(b=1,L=2,h=0.5,z_),subs(b=5,L=2,h=0.5,z_),subs(b=20,L=2,h=0.5,z_)],x=0..1.2,z=0..1);eqCat:=z=L*(H/W)*(cosh(W*x/(H*L))-1);

En efecto, el balance de fuerzas en un elemento dx de la catenaria indica que la fuerza horizantal ha de ser constante, H=cte), que la variación de la fuerza vertical debe compensar el peso de la cadena, V+dV-V=wds (siendo w el peso por unidad de longitud de cadena), y, como la fuerza resultante, T=sqrt(H^2+V^2), ha de llevar la dirección de la cadena, V/H=dz/dx, y la ecuación diferencial de la catenaria es finalmente (dV=wds) Hd2z/dx2=w*sqrt(1+(dz/dx)^2), siendo:

L=longitud entre apoyos

S=longitud de la cadena

h=flecha

theta=ángulo con la horizontal en el apoyo

H=componente horizontal de la tensión; coincide con la tensión en medio (x=0)

V=componente vertical de la tensión. La tensión tangencial es sqrt(H^2+V^2)

W=peso total soportado por la cadena.

1ª aproximación. Para cadenas tensas es una buena aproximación z=L(H/W)(x^2/2) (otra vez se ve que no vale cualquier parábola).

>	eqPar:=z=(w/H)*(x^2/2);H:=w*L^2/(4*h);

2ª aprox. Para el problema de la dilatación, también es buen modelo el de peso W concentrado enmedio (cuerda deformada triangular).

>

S:='S':h_Tri:=sqrt((S/2)^2-(L/2)^2);S_Tri:=L*(1+epsilon2^2);eqe2;h_Tri:=(L/2)*sqrt(2*epsilon2^2);h_Par:=h=W*L/(8*H);S_Par:=S=(2*H/w)*sinh(W/(2*H));h_Par:=(L/2)*sqrt(3*epsilon2^2/2);h_Cat:=(H/w)*(cosh(W/(2*H))-1);S_Cat:=S=(2*H/w)*sinh(W/(2*H));h_Cat_:='h_Par';theta[Tri]:=sqrt(2*epsilon2^2);theta[Par]:=sqrt(6*epsilon2^2);theta[Cat]:=sinh(W/(2*H));

La tensión del hilo en el punto más bajo es:

>	eqT:=sigma=T/A;T_Tri:=W/(2*sqrt(2*epsilon2^2));T_Par:=W/(2*sqrt(6*epsilon2^2));

>