>	restart:#"m04_p39"

Se tiene un depósito de 4 litros conteniendo 2 kg de CO2 a 260 K. Se pide:
a) Densidades de las fases coexistentes y fracción volumétrica de vapor (con ayuda de diagrama de propiedades, o tablas).
b) Determinar las densidades de ambas fases con el modelo de estados correspondientes.
c) Determinar la entalpía de vaporización en esas condiciones con el modelo de estados correspondientes.
d) Estado interior que se alcanzaría si se dejase atemperar en un ambiente a 35 ºC (diagrama).
e) Resolver el apartado anterior con el modelo de estados correspondientes.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="CO2":dat:=[V=0.004*m_^3,m=2*kg_,T1=260*K_,T2=(35+273)*K_];

Esquema:

>

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),get_liq_data(su),Const,SI2,SI1:get_pv_data(su):

a) Presión interior, densidades de las fases coexistentes y fracción volumétrica de vapor (con ayuda de diagrama de propiedades, o tablas).

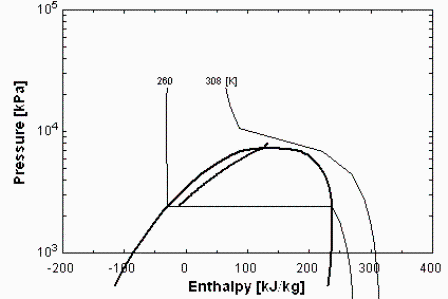
Del gráfico p-h del CO2 se obtiene, para T=260 K: pv=2,3 MPa (entre la de 2 MPa y la de 3 MPa), rho_liq=1000 kg/m3 y rho_vap=60 kg/m3.

>

p1_graf:=2.3e6*Pa_;rho_liq_graf:=1000*kg_/m_^3;rho_vap_graf:=60*kg_/m_^3;eqy:=y=Vvap/V;eqy:=y="(Vvap/m)/(V/m)";eqy:=y="(Vvap/mvap)*(mvap/m)/(V/m)";eqy:=y=(x/rho_vap)/(V/m);eqv:=v=(1-x)*vliq+x*vvap;eqv:=V/m=(1-x)/rho_liq+x/rho_vap;x_graf:=subs(rho_liq=rho_liq_graf,rho_vap=rho_vap_graf,dat,solve(%,x));eqy_graf:=subs(x=x_graf,rho_vap=rho_vap_graf,dat,eqy);

Si lo hubiéramos resuelto con el modelo de sustancia perfecta, suponiendo que está en equilibrio líquido-vapor (por la densidad media, rho=m/V=500 kg/m3).

>	eqLVE:=p1=p[v](T1);eqLVE:=p1=subs(dat,evalf(subs(dat,pv(T1))));eqMLP:=rho_liq=rho;eqMLP_:=subs(dat,%);eqMGP:=rho_vap=p1/(R*T1);eqMGP_:=subs(eqLVE,dat,%);eqy:=y=(V-Vliq)/V;;eqy:=y=(V-m/rho_liq)/V;subs(eqMLP,dat,%);

i.e., la presión interior es de 2,4 MPa (por Antoine, más aproximado que la interpolación gráfica inicial; el valor más exacto es 2,416 MPa, del NIST), y la fracción volumétrica de vapor es del 53% (la aproximación ideal da un 39%); el valor más exacto es:

>	rho_liq_NIST:=998.9*kg_/m_^3;rho_vap_NIST:=64.31*kg_/m_^3;eqs:='{Vliq+Vvap=V,mliq+mvap=m,mliq/Vliq=rho_liq_NIST,mvap/Vvap=rho_vap_NIST}';sol_:=solve(subs(dat,eqs),{mliq,mvap,Vliq,Vvap});eqy_NIST:=subs(%,dat,Vvap/V);

b) Determinar las densidades de ambas fases con el modelo de estados correspondientes.

Como ya hemos calculado las densidades con el modelo de gas ideal, basta corregir por compresibilidad.

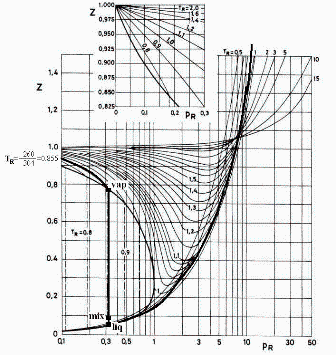
En el diagrama Z-pR se aprecia que en los límites de saturación a TR=0.85 (T=260 K), Zvap=0.78 y Zliq=0.05, luego:

>	TR:=T/T[cr];TR1:=subs(dat,T=T1,dat,%);Z1vap:=0.78;Z1liq:=0.05;eqMEC:=rho_vap='p1/(Z1vap*R*T1)';eqMEC_:=subs(eqLVE,dat,%);eqMEC:=rho_liq='p1/(Z1liq*R*T1)';eqMEC_:=subs(eqLVE,dat,%);

No está mal la rho_liq se corrige desde los 823 kg/m3 del MLP hasta casi los los 999 kg/m3 verdaderos, y la rho_vap se corrige desde los 49 kg/m3 del MGP hasta 63,4 kg/m3, cuando el valor más exacto es 64,3 kg/m3.

c) Determinar la entalpía de vaporización en esas condiciones con el modelo de estados correspondientes.

Se mira en el diagrama de correcciones por compresibilidad de la entalpía.

>	hlv:=hcc_liq-hcc_vap;hcc_liq_Tcr:=45*J_/(mol_*K_);hcc_vap_Tcr:=5*J_/(mol_*K_);hlv:='(hcc_liq_Tcr-hcc_vap_Tcr)*T[cr]/M';hlv_:=subs(dat,%);

que no se compara mal con el valor más exacto (NIST) de hvap-hliq=236,3-(-30,28)=266,6 kJ/kg.

d) Estado interior que se alcanzaría si se dejase atemperar en un ambiente a 35 ºC (diagrama).

Yendo por la curva de V=cte (rho=cte=500 kg/m3) hasta 35 ºC (308 K), se sale de la región bifásica, llegando a presión de entre 8 MPa y 9 MPa. El valor más exacto (NIST) es p2=8,098 MPa.

e) Resolver el apartado anterior con el modelo de estados correspondientes.

Por ser T2>Tcr, sabemos que sólo habrá una fase (supercrítica), pero la p2 hay que calcularla por aproximaciones porque la Z2 depende de la p2. Empecemos con p2=p1 (aunque sabemos que será mayor) y mirando la Z2(p2,T2); luego con p2=pcr, y así vamos viendo cómo queda.

>	eqBM:=m-p2*V/(Z2*R*T2)=0;TR2:=T2/T[cr];TR2_:=subs(dat,%);p2:=subs(eqLVE,p1);pR2_:=subs(dat,p2/p[cr]);Z2:=0.9;eqBM_:=subs(dat,eqBM);p2:=subs(dat,p[cr]);pR2_:=subs(dat,p2/p[cr]);Z2:=0.27;eqBM_:=subs(dat,eqBM);p2:=8e6*Pa_;pR2_:=subs(dat,p2/p[cr]);Z2:=0.22;eqBM_:=subs(dat,eqBM);

luego la solución está entre 7.4 MPa y 8 MPa; interpolando linealmente: p2=7.5 MPa (el valor exacto era 8,1 MPa).

ADICIONAL

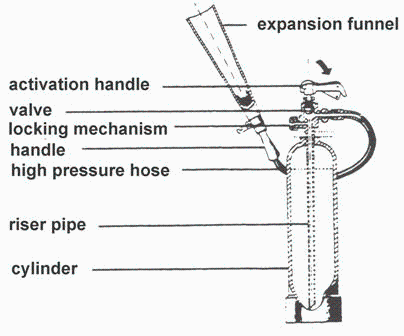
Recipientes de este tamaño, con CO2 líquido como aquí, son típicos de los extintores contra incendios manuales. Se trata de recipientes a presión (pared de 4 mm de espesor de acero) capaces de aguantar hasta unos 20 MPa.

>