>	restart:#"m04_p38"

En un matraz de cuarzo, comunicado con el exterior por un tubo capilar de 2 mm de diámetro interior, se ha dispuesto 0,500 kg de agua pesada pura (óxido de deuterio, D2O), quedando completamente lleno el matraz y hasta una cierta cota el tubo capilar, en condiciones controladas de 20 ºC, lo que corresponde según la curva de calibración a un volumen de agua destilada de 453 mL. Sabiendo que cuando se pone todo a 10 ºC el menisco desciende 97 mm, y que cuando se pone a 5 ºC (el agua pesada congela a 3,8 ºC) el menisco desciende sólo 63 mm (respecto a la cota inicial), se pide:
a) Determinar un valor típico para la densidad del agua pesada.
b) Establecer un modelo para la densidad en función de la temperatura, indicando las características más sobresalientes.
c) Determinar los coeficientes de dilatación a las temperaturas de los ensayos.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="D2O":dat:=[D=0.002*m_,m=0.5*kg_,T0=(20+273.15)*K_,V=453e-6*m_^3,T1=(10+273.15)*K_,Dz1=-97e-3*m_,T2=(5+273.15)*K_,Dz2=-63e-3*m_]:A_:=evalf(subs(dat,Pi*D^2/4)):dat:=[op(dat),A=A_];

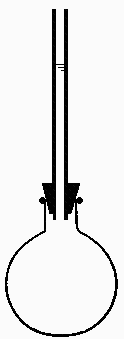
Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Determinar un valor típico para la densidad del agua pesada.

Si sabemos que la densidad del agua normal es 1000 kg/m3 y que la relación de masas molares del D2O al H2O es de 20/18, es de esperar que la densidad del agua pesada sea 1000*20/18=1111 kg/m3. Pero el enunciado nos da datos experimentales que permiten obtener directamente rho=m/V.

Sabemos la masa y el volumen inicial, luego

>	eqrho:=rho=m/V;eqrho_:=subs(dat,%);

i.e. la densidad a 20 ºC es de unos 1103 kg/m3, aunque, a juzgar por los datos aportados, la precisión no puede ser mejor del cuatro por mil (media unidad en quinientas, tanto en m como en V), luego concluimos que estará entre 1099 y 1107. En las bases de datos aparece como mejor valor a 20 ºC 1105,3 kg/m3. Para la densidad del agua normal a 20 ºC, rho=998,2 kg/m3, el modelo de volumen molar constante nos daría 998,2*20/18=1109,1 kg/m3, luego, parece que hay una ligera contracción en el volumen molar.

b) Establecer un modelo para la densidad en función de la temperatura.

Se ve que la densidad varía porque la misma masa cambia de volumen, por lo que como mínimo debemos considerar el modelo de líquid dilatable lineal, pero como vemos que no es lineal, proponemos el modelo de líquido con dilatación cúadrática (i.e. el tradicional desarrollo en serie polinómico; no conviene desarrollos superiores, por falta de datos):

>	eqrhoT:=rho=rho0*(1-alpha0*(T-T0)-(1/2)*alphaprima0*(T-T0)^2);eqalpha:=alpha=(-1/rho)*Diff(rho,T)[p];eqalpha:=alpha=alpha0+alphaprima0*(T-T0);

A la luz de los datos, entre 20 ºC y 10 ºC la dilatación media es normal, es decir al calentar dilata y al enfriar contrae; sin embargo, entre 10 ºC y 5 ºC se invierte la tendencia (i.e. aparece una anomalía como la del agua normal, que tiene densidad máxima a 4 ºC, luego el agua pesada ha de tener un valor máximo de la densidad entre 5 ºC y 20 ºC.

c) Determinar los coeficientes de dilatación a las temperaturas de los ensayos.

No conviene obtener alpha por derivación numérica de los datos, sino ajustando previamente rho(T) y luego derivando analíticamente.

También convendría operar con variaciones de densidad, en lugar de con densidades absolutas, para evitar problemas de redondeo, pero aquí no sería necesario por estar programado.

Tomando como origen el estado inicial conocido, T0=20 ºC y rho0 el calculado (1103 kg/m3), el sistema a resolver es:

>

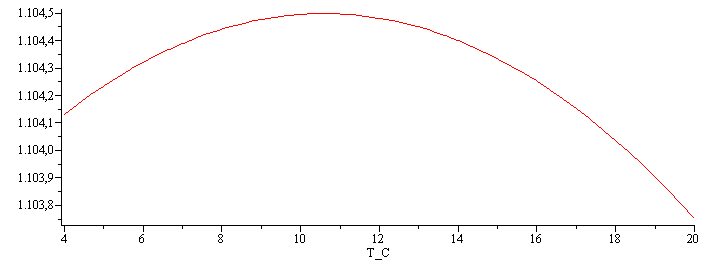
eqrhoT01:=rho1-rho0=rho0*(-alpha0*(T1-T0)-(1/2)*alphaprima0*(T1-T0)^2);eqrhoV01:=rho1-rho0=m/(V+A*Dz1)-m/V;eqrho01:=rho0*(1-A*Dz1/V)=rhs(eqrhoT01);eqrho01_:=A*Dz1/V=alpha0*(T1-T0)+(1/2)*alphaprima0*(T1-T0)^2;eqrho01__:=subs(dat,%);eqrho02_:=A*Dz2/V=alpha0*(T2-T0)+(1/2)*alphaprima0*(T2-T0)^2;eqrho02__:=subs(dat,%);sol_:=solve({eqrho01__,eqrho02__},{alpha0,alphaprima0});eqrhonum:=subs(sol_,rho0=rhs(eqrho_),dat,SI0,eqrhoT);eqalphanum:=subs(sol_,dat,SI0,eqalpha);alpha[20]=subs(T=T0,sol_,dat,rhs(eqalpha));alpha[10]=subs(T=T1,sol_,dat,rhs(eqalpha));alpha[5]=subs(T=T2,sol_,dat,rhs(eqalpha));T[alpha=0]=subs(sol_,dat,solve(rhs(eqalpha)=0,T));plot(subs(T=273.15+T_C,rhs(eqrhonum)),T_C=4..20);plot(subs(T=273.15+T_C,rhs(eqalphanum)),T_C=4..20);

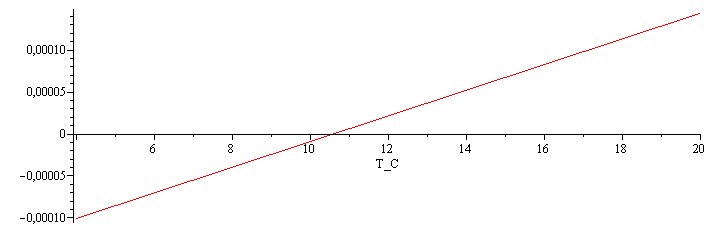i.e. alpha=144·10^-6 1/K a 20 ºC, alpha=9·10^-6 1/K a 10 ºC y alpha=-85·10^-6 1/K a 5 ºC. La dilatación sería nula cerca de los 10 ºC (283 K). En las bases de datos aparece como mejor valor rhomax=1106.0 kg/m3 a 11,2 ºC. El estudio de la incertidumbre en el valor aquí calculado (9 ºC) es mucho más complicado que el realizado para las densidades.

>