>	restart:#"m04_p32"

Supóngase que se desea estudiar los cambios de fase de una sustancia pura a partir resultados experimentales de la medida de la presión de vapor a varias temperaturas, para cada fase, como los que se presentan en la tabla adjunta para el agua. Con estos datos, se desea calcular:
a) La temperatura y presión del punto triple.
b) La entalpía de vaporización.
c) La entalpía de sublimación.
d) La entalpía de fusión.
e) La temperatura de ebullición estándar.

Estado           T [ºC] pv [mmHg]
Líquido-vapor 4 6,20
Líquido-vapor 2 5,42
Sólido-vapor -2 3,99
Sólido-vapor -4 3,32

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="H2O":dat:=[]:Tdat:=[-4,-2,2,4];pvdat:=[3.32,3.99,5.42,6.20];Tdata:=[seq((Tdat[i]+273)*K_,i=1..4)];pvdata:=[seq(pvdat[i]*1e5*Pa_/760,i=1..4)];

Ecs. const.:

>	dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):

a) La temperatura y presión del punto triple.

Empezaremos por representar los datos en un diagrama  p-T (aunque sea esquemáticamente).

Hay que representar dos curvas: la de sublimación (vaporización desde la fase sólida) y la de ebullición (vaporización desde la fase líquida). Como sólo tenemos dos puntos de cada curva, parecería lógico ajustar sendas curvas por sendas rectas, pero la Termodinámica enseña que el mejor ajuste es por exponenciales como enseña la Ec. de Clapeyron integrada: lnp=A-B/T. La experiencia enseña que el ajuste empírico de Antoine (lnp=A-B/(T+C)) es algo mejor que el de la Ec. de Clapeyron integrada, pero sólo tenemos dos puntos y por ello sólo podemos ajustar dos constantes.

Ajustando lnp=A-B/T:

>

eqClap:=ln(p)=A-B/T;eqClap4:=evalf(subs(SI0,ln(pvdata[4])=A-B/Tdata[4]));eqClap3:=evalf(subs(SI0,ln(pvdata[3])=A-B/Tdata[3]));sol_lv:=solve({eqClap3,eqClap4},{A,B});pv_lv:=subs(sol_lv,exp(A-B*K_/T))*Pa_;eqClap2:=evalf(subs(SI0,ln(pvdata[2])=A-B/Tdata[2]));eqClap1:=evalf(subs(SI0,ln(pvdata[1])=A-B/Tdata[1]));sol_sv:=solve({eqClap1,eqClap2},{A,B});pv_sv:=subs(sol_sv,exp(A-B*K_/T))*Pa_;plot([subs(sol_sv,exp(rhs(eqClap))),subs(sol_lv,exp(rhs(eqClap)))],T=269..277);

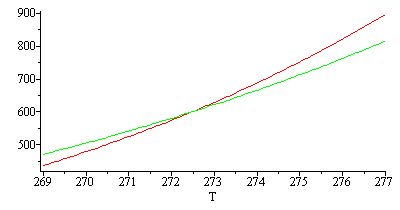La temperatura y la presión del punto triple serán las de corte de ambas curvas.

>	T_PT:=solve(pv_sv=pv_lv,T);p_PT:=evalf(subs(T=T_PT,pv_sv));

i.e. el punto triple sería T=272,5 K y p=600 Pa, cuando en realidad conocemos que para el agua pura es exactamente Ttr=273,16 K y aproximadamente ptr=611 Pa.

Ajustando linealmente se obtendría:

>	pv_lv_:='pvdata[3]+(T-Tdata[3])*(pvdata[4]-pvdata[3])/(Tdata[4]-Tdata[3])';pv_sv_:='pvdata[1]+(T-Tdata[1])*(pvdata[2]-pvdata[1])/(Tdata[2]-Tdata[1])';T_PT_:=evalf(solve(pv_sv_=pv_lv_,T));p_PT_:=evalf(subs(T=T_PT_,pv_sv_));

b) Calcular la entalpía de vaporización.

De la ec. de Clapeyron, con la aproximación de vlv=vv=RT/p:

>	eqClap_liq:=(dp/dT)[sat]=h[lv]/(T*v[lv]);eqClap_liq:=(dp/dT)[sat]=h[lv]*p/(R*T^2);eqClap_liq:=h[lv]='(R*T^2/p)*(pvdata[4]-pvdata[3])/(Tdata[4]-Tdata[3])';eqClap_liq_:=subs(T=Tdata[3],p=pvdata[3],R=R[u],Const,eqClap_liq);eqClap_liq__:=subs(T=Tdata[3],p=pvdata[3],dat,eqClap_liq);

i.e. hlv=45,2 kJ/mol (se ha hecho uso de la masa molar del agua sólo por familiaridad; en realidad, para el agua pura cerca del punto triple el valor es hlv=2500 kJ/kg=45 kJ/mol).

c) Calcular la entalpía de sublimación.

>	eqClap_sol:=(dp/dT)[sat]=h[sv]/(T*v[sv]);eqClap_sol:=(dp/dT)[sat]=h[sv]*p/(R*T^2);eqClap_sol:=h[sv]='(R*T^2/p)*(pvdata[2]-pvdata[1])/(Tdata[2]-Tdata[1])';eqClap_sol_:=subs(T=Tdata[2],p=pvdata[2],R=R[u],Const,eqClap_sol);eqClap_sol__:=subs(T=Tdata[2],p=pvdata[2],dat,eqClap_sol);

i.e. la hsv=51,3 kJ/mol (en las tablas no suele venir este valor, pero a partir de hlv y hsl se obtendría un valor experimental de hsv=2880 kJ/kg=51,8 kJ/mol).

d) Calcular la entalpía de fusión.

>	eqlim:=h[sv]=h[sl]+h[lv];h[sl]=subs(eqClap_liq_,eqClap_sol_,h[sv]-h[lv]);h[sl]=subs(eqClap_liq__,eqClap_sol__,h[sv]-h[lv]);

cuando en realidad es de unos 330 kJ/kg=5,9 kJ/mol.

e) La temperatura de ebullición estándar.

(Aquí si que la aproximación lineal sería grosera).

>	eqClap:=ln(p0/p4)=-(h[lv]/R)*(1/Tb-1/T4);Tb:=solve(%,Tb);Tb_:=evalf(subs(T4=Tdata[4],p4=pvdata[4],eqClap_liq_,R=R[u],Const,Tb));

i.e. a 100 kPa el agua herviría a 366 K (cuando en realidad lo hace a 373 K).

En conclusión, parece que los resultados tienen una incertidumbre cerca del punto crítico como cabría esperar de la incertidumbre asumida para los datos, pero la extrapolación a temperaturas altas aumneta inaceptablemente la incertidumbre

>

>