>	restart:#"m04_p31"

En un recipiente metálico de 1 litro de capacidad se tiene dióxido de carbono inicialmente a 20 ºC y 3 MPa, el cual se introduce en un baño de hielo a  ºC. Se pide:
a) Determinar la cantidad de sustancia inicial, indicando el método seguido y la incertidumbre estimada.
b) Determinar el estado final.
c) Determinar las variaciones de energía interna, entalpía y entropía entre ambos estados.
d) Calor intercambiado.
e) Indicar el proceso que sufriría el fluido interior si ocurriera un escape rápido de CO2.
f) Representar en los diagramas T-s y p-h la evolución.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="CO2":dat:=[V=1e-3*m_^3,T1=(20+273)*K_,T0=T1,p1=3e6*Pa_,T2=(0+273)*K_];

Esquema:

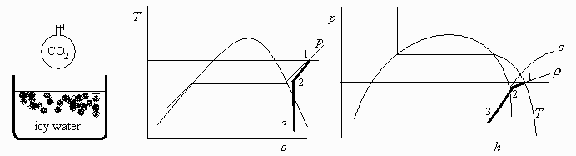
Ecs. const.:

>	dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):

a) Determinar la cantidad de sustancia inicial, indicando el método seguido y la incertidumbre estimada.

MGI:

>	eqET_MGI:=n=p*V/(R[u]*T);eqET_MGI:=n=p1*V/(R[u]*T1);eqET_MGI_:=subs(Const,dat,%);m_MGI_:=subs(eqET_MGI_,dat,n*M);p[v](T1)=subs(dat,evalf(subs(dat,pv(T1))));

i.e. habría 1,23 moles de gas (pues están a 3 MPa y a esa temperatura no condensarían hasta 5,7 MPa). Pero hay que ver si el MGI es suficientemente bueno.

MEC (la Z(p,T) se mira en el gráfico del MEC):

>	p[R1]:=p1/p[cr];pR1_:=subs(dat,%);T[R1]:=T1/T[cr];TR1_:=subs(dat,%);eqGR:=Z1=0.82;eqET_MEC:=n=p1*V/(Z1*R[u]*T1);eqET_MEC_:=subs(Const,eqGR,dat,eqET_MEC);

Gráfico p-h del CO2. A 20 ºC y 3 MPa la isocora que pasa es la de 66 kg/m3 (el valor más exacto, NIST, es de 66,19 kg/m3.

>	n_Gph:=m_Gph/M;m_Gph:=rho*V;rho_Gph_:=66*kg_/m_^3;eqET_Gph_:=n=subs(dat,rho_Gph_*V/M);

i.e., el MGI da un error del 20%, pero el MEC ya da un error menor del 1%.

b) Determinar el estado final.

La evolución será a densidad global constante (no varía la masa ni el volumen). Suponiendo que siga todo gas en esas condiciones, con el MGI:

>	T2_:=subs(dat,T2);eqBM:=p2=n*R[u]*T2/V;eqBM_:=subs(Const,eqET_MGI_,dat,%);p[v](T2)=subs(dat,evalf(subs(dat,pv(T2))));

i.e. sigue gaseoso (la presión baja de 3 MPa a 2,8 MPa, pero no condensa hasta 3,5 MPa a esa temperatura).

Con el MEC hay que resolver gráficamente el balance másico Z1*n*Ru*T1/(p1*V)=Z1(p2,T2)*n*Ru*T2/(p2*V), que se hará por aproximaciones sucesivas, empezando por la aproximación de gas ideal:

>	eq12:n1=n2;eq12:=p1*V/(Z1*R[u]*T1)=p2*V/(Z2(p2,T2)*R[u]*T2);eq12:=Z2(p2,T2)*T2*p1/(Z1*T1*p2)=1;

>	p2_:=2.8e6*Pa_;pR2:=subs(dat,p2_/p[cr]);TR2:=subs(dat,T2/T[cr]);Z2:=0.76;eq12_:=subs(eqGR,dat,Z2*T2*p1/(Z1*T1*p2_));

>	p2_:=2.6e6*Pa_;pR2:=subs(dat,p2_/p[cr]);TR2:=subs(dat,T2/T[cr]);Z2:=0.79;eq12_:=subs(eqGR,dat,Z2*T2*p1/(Z1*T1*p2_));

i.e. la p2 con el MEC es 2,7 MPa, que se compara favorablemente con el valor obtenido del gráfico p-h del CO2 (el valor más exacto es 2,68 MPa).

c) Determinar las variaciones de energía interna, entalpía y entropía entre ambos estados.

Con el MGP:

>	DU:=m*c[v]*(T2-T1);DU_:=subs(m=m_MGI_,dat,%);DH:=m*c[p]*(T2-T1);DH_:=subs(m=m_MGI_,dat,%);DS:=m*(c[p]*ln(T2/T1)-R*ln(p2/p1));DS_:=subs(dat,evalf(subs(eqBM_,m=m_MGI_,dat,%)));c[p]=subs(dat,c[p]);

Con el MEC, con ayuda de los diagramas de correcciones por compresibilidad:

>

DH:=m*(Dh12id-Dhcc2+Dhcc1);Dh_Tcr_2:=5*(J_/(mol_*K_));Dhcc2:=subs(dat,Dh_Tcr_2*T[cr]/M);Dh_Tcr_1:=4*(J_/(mol_*K_));Dhcc1:=subs(dat,Dh_Tcr_1*T[cr]/M);DH__:=DH_-m_MGI_*Dhcc2+m_MGI_*Dhcc1;DS:=m*(Ds12id-Dscc2+Dscc1);Dscc_Tcr_2:=4*(J_/(mol_*K_));Dscc2:=subs(dat,Dscc_Tcr_2/M);Dscc_Tcr_1:=3*(J_/(mol_*K_));Dscc1:=subs(dat,Dscc_Tcr_1/M);DS__:=DS_-m_MGI_*Dscc2+m_MGI_*Dscc1;DU=DH-D(pV);DU__:=DH__-subs(eqBM_,dat,V*(p2-p1));

Con los datos más exactos disponibles (NIST), los resultados serían: DH=-1344 J, DU=-1024 J y DS=3,62 J/K.

d) Calor intercambiado.

>	Q[V]='DU';Q[V]=DU__;

Nótese la importancia de las correcciones; p.e. el calor transmitido sería Q=DU=-1 kJ en vez de -0,7 kJ.

e) Indicar el proceso que sufriría el fluido interior si se ocurriera un escape rápido de CO2.

La expansión en el interior sería isoentrópica (rápida y sin fricción), y se alcanzaría la curva de vapor saturado y empezaría a condensar vapor en gotitas, justo en ese momento, o algo después si el proceso fuese metastable.

d) Representar en los diagramas T-s y p-h la evolución.

(Hecho arriba)

>