>	restart:#"m04_np26"

En una publicación se han encontrado para la presión de vapor de una sustancia pura sobre su líquido y sobre su sólido las expresiones siguientes: lnpvap=19,49-3060/T  y lnpsubl=23,03-3754/T, con p en mmHg y T en K. Se pide:
a) En que estado fásico se encontrará esa sustancia en condiciones ambiente.
b) Determinar su punto triple ¿Puede determinarse el punto crítico?
c) Determinar la entalpía de ebullición.
d) Determinar la entalpía de sublimación y la de fusión.
e) ¿De qué sustancia puede tratarse?

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(xL>0):

>	su:="NH3":dat:=[A1=19.49,B1=3060*K_,A2=23.03,B2=3754*K_];pvap:=pu*exp(A1-B1/T)*mmHg_;psubl:=pu*exp(A2-B2/T)*mmHg_;

Esquema:

>

>

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:sdat:=get_gas_data(su),get_liq_data(su):

a) En que estado fásico se encontrará esa sustancia en condiciones ambiente.

>	pu:=(1e5/760)*Pa_/mmHg_;Tb=T(pv=100*kPa_);Tb_:=evalf(subs(dat,solve(subs(dat,pvap=p0),T)));

i.e. a 100 kPa hierve a 238 K, luego a 288K es un gas.

b) Determinar su punto triple ¿Puede determinarse el punto crítico?

El punto triple será donde coincidan ambas curvas de presión de vapor.

>	eqPTR:='pvap=psubl';Ttr_:=fsolve(subs(dat,SI0,eqPTR),T=1e1..1e3)*K_;ptr_:=subs(dat,evalf(subs(T=Ttr_,dat,pvap)));

Esta temperatura del punto triple será prácticamente la misma que la de congelación.

El punto crítico no se puede saber porque no nos dan el límite de aplicación de la curva de presión de vapor. Sin embargo, podría obtenerse una estimación combinando los datos de presión de vapor con la aproximación de Guggenheim basada en el modelo de estados correspòndientes, lnpR=K(1-1/TR, con K=6, o con la aproximación empírica Ttr/Tcr=0,6.

>

eqGugg:=ln(p/pcr)=K*(1-Tcr/T);eqGugg_:=ln(p)=ln(pcr)+K*(1-Tcr/T);eqDAT:=ln(p)=ln(pu*mmHg_)+A1-B1/T;eq1:=ln(pcr)+K=ln(pu*mmHg_)+A1;eq2:=K*Tcr=B1;pcr_:=subs(dat,evalf(subs(K=6,dat,pu*mmHg_*exp(A1)/exp(K)))):'pcr'=evalf(%,2);Tcr_:=subs(K=6,dat,B1/K);eq0:=Ttr/Tcr=0.6;Tcr_:=Ttr_/0.6;pcr_:=subs(dat,evalf(subs(T=Tcr_,dat,pvap))):'pcr'=evalf(%,2);

Ya se ve que estas estimaciones tienen gran indertidumbre (del orden del 30% en temperaturas).

c) Determinar la entalpía de ebullición.

>	eqClapeyron:=dp/dT=Dh/(T*Dv);eqClapeyron:=p/p0=exp(-(hlv/R[u])*(1/T-1/Tb));eqClapeyron_T:=dlnpvap/dT=diff(-(hlv/R[u])*(1/T-1/Tb),T);dlnpvap_T:=diff(ln(pvap),T);eq_hlv:=rhs(eqClapeyron_T)=subs(dat,%);hlv_:=subs(dat,solve(%,hlv));

Como no sabemos la masa molar, sólo podemos determinar la entalpía molar.

d) Determinar la entalpía de sublimación y la de fusión.

>	eq_hsv:=hsv/(R[u]*T^2)=B2/T^2;hsv_:=subs(dat,solve(subs(dat,%),hsv));hsl:=hsv-hlv;hsl_:=hsv_-hlv_;

e) ¿De qué substancia puede tratarse?

Mirando simplemente su punto de ebullición (238 K), los más próximos son el propano (Tb=231 K) y el amoníaco (Tb=240 K); de la temperatura de fusión (196 K) se deduce finalmente que sería amoníaco (Tf=195 K, frente a Tfpropano=83 K). Se puede ahora comprobar los otros valores hallados.

>

ADDICIONAL. Comparación con los datos tabulados del amoníaco y representación gráfica.

>	eqCheck_Ttr:=evalf(subs(sdat,Ttr_=T[f]),3);eqCheck_Tcr:=evalf(subs(sdat,Tcr_=T[cr]),3);eqCheck_pcr:=evalf(subs(sdat,pcr_=p[cr]),3);eqCheck_hlv:=evalf(subs(sdat,hlv_/M=h[lv0]),3);eqCheck_hsl:=evalf(subs(sdat,hsl_/M=h[sl0]),3);

i.e., coincide bien con los datos del libro excepto los valores del punto crítico, como ya se esperaba (es Tcr=406 K y las estimaciones eran de 330 K y 510 K) .

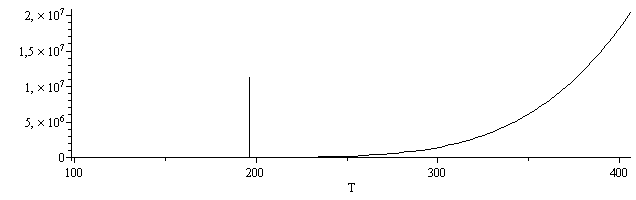
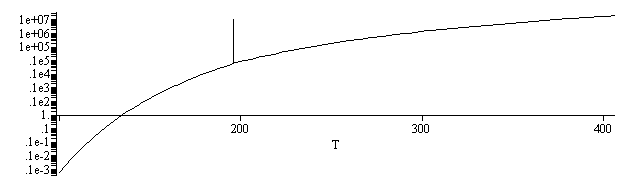
>	p_T:=evalf(subs(dat,sdat,SI0,piecewise(T>Ttr_,pvap,psubl)));plot(subs(sdat,SI0,{[[Ttr_,ptr_],[Ttr_,p[cr]]],p_T}),T=100..406,color=black);with(plots):logplot(subs(sdat,dat,SI0,{[[Ttr_,ptr_],[Ttr_,p[cr]]],p_T}),T=100..406,color=black);

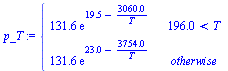NOTA: Nótese que el dato de la pvap sólo es bueno a presiones bajas; cerca del punto crítico va muy mal: para Tcr=406 K, da pcr=20 MPa cuando el valor tabulado es de 11 MPa.

>