>	restart:#"m04_p24"

Se quiere expulsar 10 toneladas de agua de lastre de un submarino a 100 m de profundidad, disponiendo de un depósito rígido con aire a 15 MPa, según se esquematiza en la figura. Se pide:
a) Determinar el trabajo necesario y la cantidad de aire para conseguirlo.
b) Volumen mínimo del depósito de aire.
c) Exergía del aire anterior respecto al aire atmosférico.
d) Considérese que la descarga es rápida y determínese la expresión general para la variación de la temperatura con la presión en un proceso isoentrópico, particularizándolo al caso del aire y del agua.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[mw=10e3*kg_,z1=100*m_,p1=15e6*Pa_];

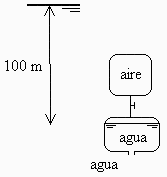
Esquema:

>

>

Ecs. const.:

>	gdat:=get_gas_data(su1):dat:=op(dat),Const,gdat,SI2,SI1:Wdat:=get_liq_data(su2):

a) Determinar el trabajo necesario y la cantidad de aire para conseguirlo.

Todo el volumen ocupado por el agua de lastre habrá de ser desplazado por el aire (que deberá estar a más presión).

Tomaremos para el agua de mar las mismas propiedades del agua pura incompresible, y para el aire el modelo de gas perfecto.

Consideraremos que la temperatura a 100 m de profundidad es 15 ºC; en realidad puede ser de hasta -1 ºC en las aguas polares y hasta 25 ºC en las tropicales, siendo de unos 10 ºC en las zonas templadas, pero apenas cuenta aquí.

Para desplazar el agua (10 t ocupan Vw=10 m3), sin que entre más agua al volumen de control, éste deberá sufrir una expansion de volumen Vw contra una presión pw (que a 100 m será aprox. 1,1 MPa; 10 m 100 kPa), i.e. W=pw*Vw=11 MJ.

Para ello se necesita rellenar 10 m3 con aire a 1,1 MPa, unos 110 kg (a 1 kg/m3 STP), que a 15 MPa ocupan 10*1,1/15=0.73 m3.

Ahora lo calculamos mejor:

>	Wmin:=pw*Vw;T1=T0;eqDespl:=Va=Vw; eqBM:=pa=pw;Vw:=mw/rho;Vw_:=subs(Wdat,dat,Vw);pw:=p0+rho*g*z1;pw_:=subs(dat,subs(Wdat,dat,pw));eqma:=ma=pa*Va/(R*T);ma_:=subs(dat,pw_*Vw_/(R*T0));Wmin_:=subs(dat,pw_*Vw_);

b) Volumen mínimo del depósito de aire

Algo más de los 0,73 m3 del aire de empuje, pues ha de quedar el resto como mínimo a pw.

Al final el depósito deberá quedar como mínimo a una presión pw.

>	eqma2:=ma_total=ma_dep+ma_tan;'ma_tan'=evalf(ma_);ma_dep:='pw*Vd/(R*T0)';ma_total:='p1*Vd/(R*T0)';Vd_:=solve(eqma2,Vd);Vd__:=subs(ma_tan=ma_,Wdat,dat,Vd_);ma_dep_:=subs(Vd=Vd__,Wdat,dat,ma_dep);ma_total_:=subs(Vd=Vd__,Wdat,dat,ma_total);

c) Exergía del aire anterior respecto al aire atmosférico.

>	Wmax:=DE+p0*DV-T0*DS;DE:=0;p0DV:=p0*V0-p0*Vd;p0DV_:=subs(dat,ma_total_*R*T0-p0*Vd__):'p0DV'=evalf(%,2);T0DS:='-T0*ma_total*R*ln(p0/pw)';T0DS_:=subs(dat,evalf(subs(Vd=Vd__,Wdat,dat,-T0*ma_total*R*ln(p0/pw)))):'T0DS'=evalf(%,2);Wmax_:=p0DV_-T0DS_:'Wmax'=evalf(%,2);

i.e. ese aire sería capaz de desarrollar 16 MJ como máximo (el signo indica que el estado final tiene menos exergía), y se va a usar para realizar 11 MJ.

d) Considérese que la descarga es rápida y determínese la expresión general para la variación de la temperatura con la presión en un proceso isoentrópico, particularizándolo al caso del aire y del agua.

Los cálculos anteriores corresponderían a un proceso lento para poder considerar que la temperatura del aire no varía. Si el proceso es rápido, el aire en el depósito sufrirá una despresurización casi isoentrópica, por lo que la masa fría de aire que va saliendo y la que quedase al acabar de tirar lastre serían mayores que en el caso isotermo, y por tanto se necesitaría una cantidad inicial mayor de aire (un depósito más grande), para conseguir el mismo fin (más rápidamente).

>	eqds:=ds=c[p]*dT/T-alpha*v*dp;eqdT_dp:=Diff(T,p)[s]=T*alpha/(rho*c[p]);eqMGP:=subs(alpha=1/T,rho=p/(R*T),%);eqMGP:=Diff(lnT,lnp)[s]=(gamma-1)/gamma;eqMGP:=T/T0=(p/p0)^((gamma-1)/gamma);T2:=T1*(pw/p1)^((gamma-1)/gamma);T2_:=subs(T1=T0,Wdat,dat,T2);eqMLP:=subs(alpha=0,eqdT_dp);

i.e. en la expansión isoentrópica de una sustancia la temperatura puede aumentar o disminuir según sea alpha (las otras son positivas). En el caso de gases perfectos se obtiene el resultado conocido (T/T0)=(p/p0)^((gamma-1)/gamma), con lo que el aire se enfriaría desde 288 K hasta 136 K. En el caso de los líquidos perfectos no habría efectos térmicos al ser alpha=0, pero en la realidad alpha(agua de mar a 288 K)=0,2x10^-3 1/K y por tanto (dT/dp)s=0,014 K/MPa, i.e. apenas se enfriaría 0,014 ºC al subir rápidamente desde 100 m de profundidad a la superficie (sin embargo, en otras aplicaciones como en la de preserbación de alimentos por golpe de alta presión, el incremento de temperatura es de 3 ºC al comprimir agua a 25 ºC desde 100 kPa a 100 MPa, y aún más si la prensa es de aceite y no de agua).

>	dT_dp_:=subs(T=T0,alpha=200e-6/K_,c[p]=c,Wdat,dat,SI0,rhs(eqdT_dp))*K_/Pa_:eqWater:=lhs(eqdT_dp)=evalf(%,2);

>