| > | restart;#"m04_p23" |
Se propone el modelo siguiente para describir el comportamiento termodinámico de una cierta substancia: v(T,p)=T(AT+B/p), cp(T,p)=C+DT+ETp, con A, B, C, D y E constantes propias a determinar experimentalmente. Se pide:
a) Determinar si dicho modelo puede ser coherente (i.e. admite todas esas constantes independientes).
b) Determinar cv(T,p), en función de las constantes.
c) Coeficiente de Joule-Thomson.
d) Variaciones de entropía..
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | eq1:=v=T*(A*T+B/p);eq2:=c[p]=C+D*T+E*T*p; |
a) Determinar si dicho modelo puede ser coherente (i.e. admite todas esas constantes independientes
La variación de cp con p habrá de estar relacionada con la de v con T.
| > | eqv:=dv=alpha*v*dT-kappa*v*dp;eqs:=ds=(c[p]/T)*dT-alpha*v*dp;eq3:=Diff((c[p]/T),p)=Diff(-alpha*v,T);eq3_:=Diff(c[p],p)/T=-Diff(Diff(v,T),T);eq3_data:=value(subs(eq1,eq2,eq3_)); |
i.e., ha de ser necesariamente E=-2A, luego, sobraba uno de estos dos parámetros.
Por otra parte, para que tienda al modelo de gas ideal a presiones bajas, ha de ser B=R (constante de los gases).
b) Determinar cv(T,p) en función de las constantes.
| > | eqMayer:=c[p]-c[v]=alpha^2*T*v/kappa;eqa:=alpha=(1/v)*Diff(v,T);eqa_:=value(subs(eq1,eqa));eqk:=kappa=(-1/v)*Diff(v,p);eqk_:=value(subs(eq1,eqk));eqcv:=subs(eqa_,eqk_,eq2,eq3_data,eqMayer);'c[v]'=collect(expand(simplify(subs(eq1,eq3_data,solve(%,c[v])))),p);lhs(eqMayer)=subs(%,eq2,B=R,lhs(eqMayer)); |
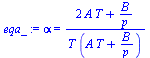 |
![`:=`(eqcv, `+`(C, `*`(D, `*`(T)), `-`(`*`(2, `*`(A, `*`(T, `*`(p))))), `-`(c[v])) = `/`(`*`(`^`(`+`(`*`(2, `*`(A, `*`(T))), `/`(`*`(B), `*`(p))), 2), `*`(v, `*`(`^`(p, 2)))), `*`(T, `*`(`+`(`*`(A, `*`...](images/np23_13.gif) |
Nótese que si A es cero (lo cual obliga a que sea E también cero), se recupera el modelo de gas ideal y cp-cv=R.
c) Coeficiente de Joule-Thomson.
| > | mu:=(dT/dp)[h];mu:=-(1-alpha*T)*v/c[p];mu_:=simplify(subs(eqa_,eq1,eq2,eq3_data,mu)); |
d) Variaciones de entropía.
| > | eqs;eqds:=expand(subs(eqa_,eq1,eq2,eq3_data,eqs));s_s0:=C*ln(T/T0)+D*(T-T0)-2*A*(p*T-p0*T0)-B*ln(p/p0);#eqds_:=expand(diff(%,T)*dT+diff(%,p)*dp); |