>	restart:#"m04_p21"

Considérese la siguiente ecuación de estado para el agua:

con r0=1000 kg/m3, a0=-0.076 kg/m3, a1=0.038 (kg/m3)/K, a2=-0.0048 (kg/m3)/K2, a3=6×10-6 (kg/m3)//K3, b=0.45×10-6 (kg/m3)/Pa, T0=273 K y p0=100 kPa. Se pide:
e) ¿Qué datos adicionales serían necesarios para tener un modelo termodinámico completo?.
f) Determinar el valor máximo de la densidad del agua de mar a 10 km de profundidad aplicando el modelo anterior, comentando las deficiencias.
g) Determinar   a 0 ºC y 100 kPa y explicar su significado físico.
h) Determinar la velocidad del sonido  .
i) ¿A qué profundidad se alcanzaría la presión crítica?

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":dat:=[rho0=1000*kg_/m_^3,a0=-0.076*kg_/m_^3,a1=0.038*kg_/(m_^3*K_),a2=-0.0048*kg_/(m_^3*K_^2),a3=6e-6*kg_/(m_^3*K_^3),b=0.45e-6*kg_/(m_^3*Pa_),T0=273*K_,z10=10e3*m_];i:='i':rho:=rho0+sum('a||i'*(T-T0)^i,i=0..3)+b*(p-p0);

Esquema:

>

>

Eqs. constit.:

>	gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):dat:=op(dat),ldat,gdat,Const,SI2,SI1:

a) ¿Qué datos adicionales serían necesarios para tener un modelo termodinámico completo?.

Falta el cp(T,p0).

En principio se supondrá el mar isotermo.

b) Determinar el valor máximo de la densidad del agua de mar a 10 km de profundidad aplicando el modelo anterior, comentando las deficiencias.

>	eqHS:=p=p0+rho0*g*z;

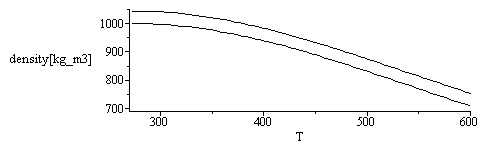
>	plot([subs(p=p0,dat,SI0,rho),subs(p=p0+rho0*g*z10,dat,SI0,rho)],T=273..600,density[kg_m3]=700..1050,color=black);Trhomax:=evalf(min(solve(subs(dat,SI0,diff(rho,T)=0),T)),3)*K_;rhomax:=evalf(subs(T=Trhomax,p=p0+rho0*g*z10,dat,rho));

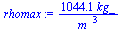Como la dependencia con T estaba separada de la de p y la de la Salinidad, sigue siendo a 4 ºC la rhomax y vale 1000 kg/m3, pero en realidad la rho del agua salada del mar no tiene máximo relativo (véase más abajo).

c) Determinar   a 0 ºC y 100 kPa y explicar su significado físico.

>	ds:=c[p]/T*dT-alpha*v*dp;dT_dp_s:=alpha*v*T/c[p];dT_dp_s:=diff(v(T),T)*T/c[p];dT_dp_s:=(-diff(rho,T)/rho^2)*T/c[p];dT_dp_s_:=subs(T=T0,p=p0,dT_dp_s);dT_dp_s__:=subs(c[p]=c,T=T0,p=p0,dat,SI0,dT_dp_s)*K_/Pa_:'dT_dp_s__'=evalf(%,2);

dT/dp a s=cte es la variación de temperatura originada por un cambio brusco de presión. Si el Dp=-100 MPa (subida adiabática de agua abisal a la superficie) sería DT=0,25 ºC. El signo indica que al subir el agua se calentaría, aunque esto es con el modelo de agua dulce (véase más abajo un modelo mejor para el agua de mar).

d) Calcular la velocidad del sonido, c_(_p/_r)s)1/2,

>	c:=evalf(sqrt(1/diff(subs(dat,rho),p)));

e) ¿A qué profundidad se alcanzaría la presión crítica?

>	pcr_:=subs(dat,p[cr]);zpcr_:=evalf(subs(dat,p=pcr_,dat,SI0,solve(eqHS,z)))*m_;

No es necesario tomar la eqHS exacta:

>	eqHS:=dp/dz='rho'*g;eqHS:='dp/rho'=g*dz;eqHS:=int(1/rho,p=p0..pcr)=g*zpcr;zpcr_:=evalf(subs(pcr=pcr_,T=T0,dat,SI0,solve(eqHS,zpcr)))*m_;

NOTA. Un mejor modelo de la densidad del agua de mar, válido entre 0 ºC y 40 ºC y para una salinidad del 3,5%, es:

>	SWdat:=[rho0=1000*kg_/m_^3,a0=28.2*kg_/m_^3,a1=-0.085*kg_/(m_^3*K_),a2=-0.0043*kg_/(m_^3*K_^2),b=0.45e-6*kg_/(m_^3*Pa_),T0=273*K_];i:='i':rho_seawater:=rho0+sum('a||i'*(T-T0)^i,i=0..2)+b*(p-p0);

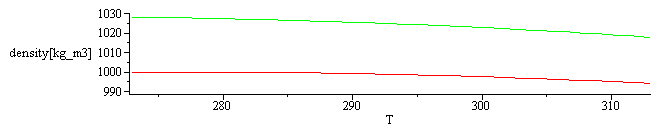
>	plot({subs(p=p0,dat,SI0,rho),subs(p=p0,SWdat,dat,SI0,rho_seawater)},T=273..313,density[kg_m3]=990..1030);

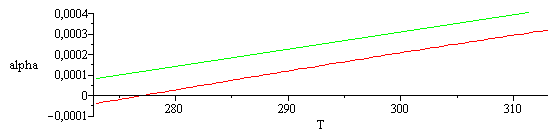
>	plot({subs(p=p0,dat,SI0,(-diff(rho,T)/rho)),subs(p=p0,SWdat,dat,SI0,(-diff(rho_seawater,T)/rho_seawater))},T=273..313,alpha=-1e-4..4e-4);

>	dT_dp_s__:=subs(a3=0,SWdat,c[p]=c,T=T0,p=p0,dat,SI0,dT_dp_s)*K_/Pa_:'dT_dp_s__'=evalf(%,2);

i.e. en lugar de calentarse al expandirse, el agua de mar se enfriaría a razón de 0,015 ºC/MPa (0,15 ºC/km).

>