>	restart;#"m4_p18"

Considérese la superposición longitudinal de dos varillas de igual sección, una de aluminio de coeficiente de dilatación a1=23×10-6 K-1 y longitud inicial L1 y la otra de titanio con a2=8,5×10-6 K-1 y longitud inicial L2, tal que medido en condiciones de laboratorio a T0=293 K, L1+L2=0,1 m. En condiciones de trabajo el extremo libre del aluminio va a estar a T1=100 K y el del titanio a T2=250 K, transmitiéndose calor en régimen estacionario. En función de la fracción de aluminio a=L1/(L1+L2), se pide:
a) Determinar el perfil de temperaturas en condiciones de trabajo.
b) Determinar la dilatación lineal del conjunto.

c) Determinar el valor de a que daría la misma dilatación que si las dos fueran de aluminio.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aluminio_anodizado":su2:="Titanio":dat:=[alpha[1]=23e-6/K_,alpha[2]=8.5e-6/K_,T0=293*K_,L12=0.1*m_,T1=100*K_,T2=250*K_];

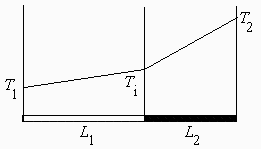
Esquema:

>

>

Eqs. constit.:

>	s1dat:=get_sol_data(su1):k_[1]:=subs(s1dat,k);s2dat:=get_sol_data(su2):k_[2]:=subs(s2dat,k);dat:=op(dat),k[1]=k_[1],k[2]=k_[2],Const,SI2,SI1:

a) Determinar el perfil de temperaturas en condiciones de trabajo.

Lineal. Sea a la fracción de aluminio.

>	eqDat:=L[1]+L[2]=L12;eqa:=a=L[1]/(L[1]+L[2]);eqBE:=k[1]*(Ti-T1)/L[1]=k[2]*(T2-Ti)/L[2];sol1_:=solve({eqDat,eqa,eqBE},{Ti,L[1],L[2]});Ti_:=subs(sol1_,Ti);Ti__:=simplify(subs(L[2]=solve(eqa,L[2]),dat,Ti_));

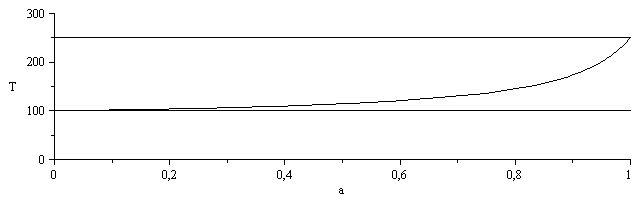
Temperatura de la unión (y las de los extremos).

>	plot(subs(dat,[T1/K_,T2/K_,Ti__/K_]),a=0..1,T=0..300,colour=black);

b) Determinar la dilatación lineal del conjunto.

La variación de longitud, supuesta pequeña, es Int(alpha*(T-T0)*dx, que si es varilla isoterma es Dx_ y si es lineal es Dx__:

>	Dx:=Int(alpha*(T-T0),x=0..L);Dx_:=collect(value(subs(T=T1,Dx)),L);Dx__:=collect(value(subs(T=A+B*x,Dx)),L);

Aluminio T=A+B*x=T1+((Ti-T1)/L1)*x

>	Dx1:=subs(L=L[1],alpha=alpha[1],A=T1,B=(Ti_-T1)/L[1],Dx__);

Titanio T=A+B*x=Ti+((T2-Ti)/L2)*x

>	Dx2:=subs(L=L[2],alpha=alpha[2],A=Ti_,B=(T2-Ti_)/L[2],Dx__);

>	Dx12_L12:='(Dx1+Dx2)/(L[1]+L[2])';Dx12_L12_:=simplify(subs(L[2]=solve(eqa,L[2]),dat,Dx12_L12));

c) Determinar el valor de a que daría la misma dilatación que si las dos fueran de aluminio.

Representando la dilatación total Dx12(_L12(a):

>	plot({Dx12_L12_,subs(a=1,Dx12_L12_),subs(a=0,Dx12_L12_)},a=0..1,dilat_m=-0.0035..0,color=black);

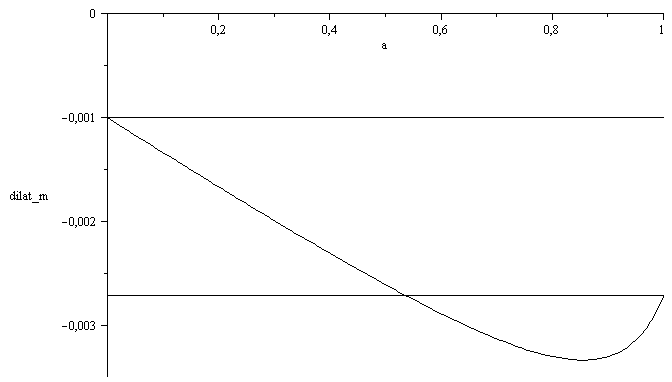se ve que hay un caso a=0,54 que dilata igual que si no hubiera titanio. También se observa un máximo de dilatación para a= 0,86.

>	a_eq_:=fsolve(Dx12_L12_=subs(a=1,Dx12_L12_),a=0..0.99):'a_eq'=evalf(%,3);Dx12_L12_eq_:=subs(a=a_sol_,Dx12_L12_):'Dx12_L12_eq'=evalf(%,2);a_max_:=fsolve(0=diff(Dx12_L12_,a),a=0..0.99):'a_max'=evalf(%,3);Dx12_L12_max_:=subs(a=a_max_,Dx12_L12_):'Dx12_L12_max'=evalf(%,2);

>