>	restart;#"m4_p17"

En un dispositivo cilindro-émbolo se tiene inicialmente una cierta cantidad de refrigerante R-134a a presión y temperatura ambientes (0,1 MPa y 15ºC). A partir de un cierto instante se comprime rápidamente la substancia hasta reducir su volumen a la décima parte del inicial y se ancla el émbolo. Se pide:
a) ¿Es apropiado el modelo de gas ideal para el estado inicial? Calcular el estado tras la compresión, con dicho modelo. ¿Es apropiado el modelo de gas ideal para ese otro estado?. Calcular el trabajo necesario para el movimiento del émbolo y el que recibe la substancia.
b) Representar esquemáticamente la evolución en el diagrama p-h.
c) Calcular el estado termodinámico en el que aparecería mezcla bifásica.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="CF3CH2F":dat:=[V2_V1_=1/10];

Esquema:

>

>

Eqs. constit.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su):dat:=op(dat),gdat,Const,SI2,SI1:get_pv_data(su):

a) ¿Es apropiado el modelo de gas ideal para el estado inicial? Calcular el estado tras la compresión, con dicho modelo. ¿Es apropiado el modelo de gas ideal para ese otro estado?.

>	T1:=T0:p1:=p0:T[cr_]:=subs(dat,T[cr]);p[cr_]:=subs(dat,p[cr]):'p[cr]'=evalf(%/(1e6*Pa_/MPa_));pR1_:=subs(dat,p1/p[cr_]);TR1_:=subs(dat,T1/T[cr_]);Z1_:=0.98;rho1_:=subs(dat,p1/(Z1_*R*T1));v1_:=1/rho1_;

El MGI es aceptable para el estado inicial (98%).

>	p2:=p1*(V1/V2)^gamma;T2:=T1*(V1/V2)^(gamma-1);p2_:=subs(dat,p1/V2_V1_^gamma):'p2'=evalf(%/(1e6*Pa_/MPa_),3);T2_:=subs(dat,T1/V2_V1_^(gamma-1));pR2_:=subs(dat,p2_/p[cr_]):'pR2'=evalf(%,2);TR2_:=subs(dat,T2_/T[cr_]):'TR2'=evalf(%,3);Z2_:=0.83;

El MGI ya no es tan bueno para el estado final (83%).

>

W12:=Int(p1*(V1/V)^gamma,V=V1..V2);W12:=value(W12);W12:='(p1*V1-p2*V2)/(gamma-1)';W12_:=subs(p2=p2_,V2=V1*V2_V1_,dat,kg_=J_*s_^2/m_^2,W12):'W12'=evalf(%,6);m1:=subs(p=p1,T=T1,V=V1,solve(eqET,m));W12_m1_:=W12_/subs(dat,m1):'W12_m1'=evalf(%/(1000*J_/kJ_),2);Wemb:='W12+Watm';Wemb:=W12-p0*(V2-V1);Wemb_m1_:=subs(V2=V1*V2_V1_,dat,Wemb/m1):'Wemb_m1'=evalf(%/(1000*J_/kJ_),2);

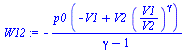La corrección por compresibilidad Du=Dh-D(pv) sería del orden de -hcc2

>	hcc2_:=3*(J_/(mol_*K_))*T[cr_]/subs(dat,M):'hcc2'=evalf(%/(1000*J_/kJ_),2);

que es una corrección del (11/60)%=17%, como en la Z.

b) Representar esquemáticamente la evolución en el diagrama p-h.

>

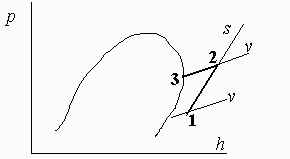
c) Calcular el estado termodinámico en el que aparecería mezcla bifásica.

En realidad el estado 2 se determinaría con las ecuaciones v2(T2,p2)=10*v1 y s2(T2,p2)=s1, mientras que el punto 3 se determinaría de v3(T3,p3)=v2 y p3=pv(T3), aunque en primera aproximación vale como se ha hecho aquí e incluso con el MGI (excepto para la pv(T)).

>	eq1:='Z2*R*T2/p2=Z3*R*T3/p3';T3_:=evalf(T2_*(p3/p2_),3);eq2:=p3=pv(T3_);p3_:=fsolve(subs(SI0,eq2),p3=1e4..1e7)*Pa_:'p3'=evalf(%/(1e6*Pa_/MPa_),2);T3_:=T2_*(p3_/p2_);

Las correcciones por compresibilidad serán aún mayores:

>	pR3_:=subs(dat,p3_/p[cr_]);TR3_:=subs(dat,T3_/T[cr_]):'TR3'=evalf(%,2);Z3_:=0.80;

>