>	restart:#"m04_p09"

4.9. Sabiendo que la densidad del agua líquida en un cierto intervalo de presiones y temperaturas puede aproximarse por:



con r0=1000 kg/m3, a0=-0,076 kg/m3, a1=0,038 (kg/m3)/K, a2=-0,0048 (kg/m3)/K, a3=6×10-6 (kg/m3)/K3, b=0,45×10-6 (kg/m3)/Pa, T0=273 K y p0=100 kPa, se pide:
a) Calcular k y a  en los puntos (0 °C, 100 kPa) y (40 °C, 100 kPa), y donde se anula a.

b) Calcular la velocidad del sonido, c_(_p/_r)s)1/2,.

c) Presión que se alcanzaría en un recipiente rígido de 1 m3, lleno de agua a 15 °C y 100 kPa al elevar la temperatura a 25 °C.

d) Volumen que debería tener un fuelle de expansión a presión ambiente para compensar esa dilatación.

Datos:

>	su:="H2O":rho:=rho0+sum('a||i'*(T-T0)^i,i=0..3)+b*(p-p0);dat:=[rho0=1000,a0=-0.076,a1=0.038,a2=-0.0048,a3=6e-6,b=0.45e-6,T1=(15+273)*K_,V15=1*m_^3,T2=(25+273)*K_];gdat:=get_gas_data(su):

Gráficos (puede compararse con datos experimentales, e.g. rho_300C=710 kg/m3, rho_cr(374 C)=320 kg/m3). En grados Celsius!

>

v='1/rho';v:=1/subs(dat,rho):alpha='(1/v)*diff(v,T)';alpha:=subs(dat,(1/v)*diff(v,T)):plot({[T,917,T=-50..0],[T,subs(T0=0,p=p0,subs(dat,rho)),T=0..374]},T=-30..374,rho_=700..1000,color=black);plot([T,subs(T0=0,p=p0,v),T=0..50],T=-5..15,v_=1e-3..1e-3+5e-7,color=black);plot({[T,0.16e-3,T=-50..0],[T,subs(T0=0,p=p0,subs(dat,alpha)),T=0..350]},T=-20..150,alpha_=-1e-4..1e-3,color=black);

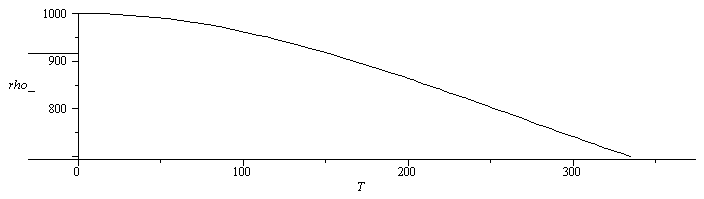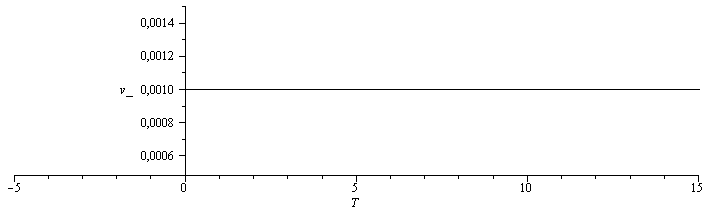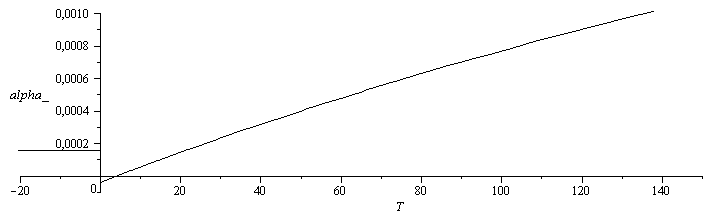a) Calcular k y a en los puntos (0 °C, 100 kPa) y (40 °C, 100 kPa), y donde se anula a.

>

Tvmin:=fsolve(subs(T0=0,p=p0,alpha)=0,T)*K_;v0:=evalf(subs(T=0,T0=0,p=p0,v),5)*m_^3/kg_;v40:=evalf(subs(T=40,T0=0,p=p0,v),5)*m_^3/kg_;vvmin:=evalf(subs(T=Tvmin/K_,T0=0,p=p0,v))*m_^3/kg_:'vvmin'=evalf(%,2);alpha0:=evalf(subs(T=0,T0=0,p=p0,alpha),2)/K_;alpha40:=evalf(subs(T=40,T0=0,p=p0,alpha),2)/K_;kappa0:=evalf(subs(T=0,T0=0,p=p0,subs(dat,(-1/v)*diff(v,p))),2)/Pa_;

b) Calcular la velocidad del sonido, c_(_p/_r)s)1/2,

>	c:=sqrt(1/Diff('rho(p)',p));c:=sqrt(1/diff(subs(dat,rho),p))*m_/s_;

c) Presión que se alcanzaría en un recipiente rígido de 1 m3, lleno de agua a 15 °C y 100 kPa al elevar la temperatura a 25 °C.

>	v15:=evalf(subs(T=(T1/K_-273),T0=0,p=p0,dat,v),5)*m_^3/kg_;m15:='V15/v15';m15_:=evalf(subs(dat,m15));p25:=fsolve(subs(T=(T2/K_-273),T0=0,p0=1e5,dat,v)=v15*kg_/m_^3,p)*Pa_:'p25'=evalf(%/(1e6*Pa_/MPa_));

d) Volumen que debería tener un fuelle de expansión a presión ambiente para compensar esa dilatación.

>	v25:=evalf(subs(T=25,T0=0,p=p0,v))*m_^3/kg_;V25:='m15*v25';V25:=evalf(m15_*v25);DV:=subs(dat,m15_*(v25-v15)):'DV'=evalf(DV,2);

Si se hubiese tomado un alpha cte e.g. a 15 ºC.

>	alpha15:=subs(T=15,T0=0,p=p0,alpha)/K_:'alpha15'=evalf(%,2);DV_:=evalf((25-15)*alpha15,2)*K_*m_^3;

>