>	restart:#"m04_p06"

Se trata de comparar el modelo de estados correspondientes aplicado al agua, con sus propiedades reales dadas por el diagrama de Mollier. Se pide:

a) Especificar todos los datos del agua que se van a usar para tener un modelo completo (aunque aproximado) de su comportamiento termodinámico (como sistema simple compresible) con dicho modelo.

b) Aproximar la curva de presión de vapor del modelo de estados correspondientes mediante la ecuación lnpR=K(1 1/TR), determinando K por ajuste en el punto TR=0,75.

c) Calcular la temperatura de vaporización a 1 MPa con dicho modelo y comparar el resultado con los datos reales.

d) Aproximar la curva de entalpía de vaporización en función de la temperatura que se obtendría del modelo de estados correspondientes, por la expresión hlv/RTcr= A(1 TR)1/3, determinando A por ajuste en el punto TR=0,75, y compararla con la expresión lineal del modelo de sustancias perfectas.

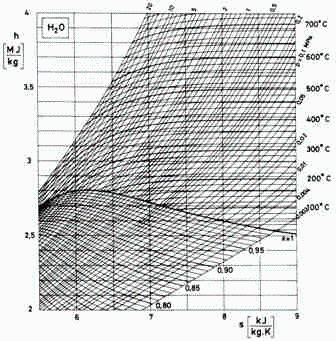
e) Calcular hlv a 1 MPa con el modelo anterior y compararlo con el del diagrama de Mollier.

f) Indicar cómo se calcularía el punto de máxima entalpía de la línea de saturación en el diagrama h s con dicho modelo.

g) Calcular el punto anterior y compararlo con los datos del diagrama de Mollier.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":gdat:=get_gas_data(su):ldat:=get_liq_data(su):dat:=gdat,ldat,Const,SI2,SI1:

a) Especificar todos los datos del agua que se van a usar para tener un modelo completo (aunque aproximado) de su comportamiento termodinámico (como sistema simple compresible) con dicho modelo.

El gráfico Z pR y sus derivados hid h y sid s, Tcr, pcr, M y cp(T,p0).

b) Aproximar la curva de presión de vapor del modelo de estados correspondientes mediante la ecuación lnpR=K(1 1/TR), determinando K por ajuste en el punto TR=0,75.

Mirando en el diagrama Z-pR para TR=0,75:

>	TR75:=0.75;pR75:=0.11;eqG:=ln(pR)=K*(1-1/TR);K:=solve(subs(pR=pR75,TR=TR75,eqG),K):'K'=evalf(%,2);

c) Calcular la temperatura de vaporización a 1 MPa con dicho modelo y comparar el resultado con los datos reales.

>	Tv1M:=subs(dat,T[cr])*solve(subs(pR=1e6*Pa_/subs(dat,p[cr]),eqG),TR);Ttermopro:=(180+273)*K_;

d) Aproximar la curva de entalpía de vaporización en función de la temperatura que se obtendría del modelo de estados correspondientes, por la expresión hlv/RTcr= A(1 TR)1/3, determinando A por ajuste en el punto TR=0,75, y compararla con la expresión lineal del modelo de sustancias perfectas

>

hccliq75:=subs(dat,(51*J_/(mol_*K_))*T[cr]/M):'hccliq75'=evalf(%/(1e3*J_/kJ_));hccvap75:=subs(dat,(2*J_/(mol_*K_))*T[cr]/M):'hccvap75'=evalf(%/(1e3*J_/kJ_));hlv75:=hccliq75-hccvap75:'hlv75'=evalf(%/(1e3*J_/kJ_));eqhlv:=hlv/(R*T[cr])=A*(1-TR)^(1/3);A_:=solve(subs(hlv=hlv75,TR=TR75,dat,eqhlv),A);plot([subs(dat,SI0,10*R*T[cr]*(1-T/T[cr])^(1/3)),subs(dat,SI0,hlv(T))],T=273..subs(dat,SI0,T[cr]),hlv=0..2.5e6,color=black);

La aproximación por el MEC no es muy buena para el agua porque su Zcr=0,23 y para el MEC se eligió Zcr=0,27.

e) Calcular hlv a 1 MPa con el modelo anterior y compararlo con el del diagrama de Mollier.

>	hlv1M:=subs(dat,solve(subs(TR=Tv1M/T[cr],dat,eqhlv),hlv)):'hlv1M'=evalf(%/(1e6*J_/MJ_),3);hlvtermopro:=(2778e3-763e3)*J_/kg_:'hlvtermopro'=evalf(%/(1e6*J_/MJ_),3);

f) Indicar cómo se calcularía el punto de máxima entalpía de la línea de saturación en el diagrama h s con dicho modelo.

La entalpía del vapor saturado a temperatura T será h(T)=href+c*(T-Tref)+hlv(T), y el máximo se calcularía derivando e igualando a cero.

>	h:='h0+cpliq*(T-T0)+R*Tcr*A*(1-T/Tcr)^(1/3)';eq0:=diff(h,T);

g) Calcular el punto anterior y compararlo con los datos del diagrama de Mollier.

>	cpliq:=subs(dat,c):eq0_:=expand(subs(A=A_,Tcr=T[cr],dat,SI0,eq0));Thmax_:=solve(eq0_,T)[1]*K_;Thmax_data:=(230+273)*K_;hmax_:=evalf(subs(A=A_,dat,J_=1e-6*MJ_,subs(Tcr=T[cr],dat,T=Thmax_,h)),3);hmax_data:=2.80*MJ_/kg_;

>