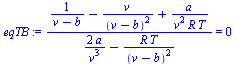>	restart:#"m04_p05".

Se va a hacer uso de la ecuación de van der Waals con las constantes determinadas a partir de las condiciones en el punto crítico, en lugar de por ajuste en una zona más amplia. Se pide:
a) Calcular a, b y R en función de Tcr, pcr y vcr.
b) Calcular a, b y vcr en función de Tcr, pcr y R. Esto es mejor porque así la R corresponde a la de los gases ideales y porque la vcr tiene gran incertidumbre experimental.
c) Expresión del factor de compresibilidad en función de las magnitudes reducidas.
d) Expresar la presión reducida en función de las otras magnitudes reducidas.
e) Puntos en los que las isotermas son horizontales en el diagrama Z-p y temperatura de Boyle, y comparación con la del diagrama generalizado de compresibilidad.
f) Curva de inversión y temperatura de inversión, y comparación con la del diagrama generalizado de compresibilidad.
g) Repetir el problema para otras ecuaciones de estado:Dietericci, Redlich-Kwong, Berthelot).
Datos:

>	eq1:=Z=v/(v-b)-a/(v*R*T);#van der Waals

>	#eq1:=Z=(v/(v-b))*exp(-a/(v*R*T));#Dieterici

>	#eq1:=Z=v/(v-b)-a/((v+b)*R*T^(3/2));#Redlich-Kwong

>	#eq1:=Z=v/(v-b)-a/(v*R*T^2);#Berthelot

>	eq2:=Z=p*v/(R*T);

a) Calcular a, b en función de Tcr y pcr.

>	assign(eq1):p:=subs(v_b=v-b,collect(subs(v=v_b+b,solve(eq2,p)),a));

>	ppri:=diff(p,v):psec:=diff(ppri,v):

>	sol1:=solve(subs({T=Tcr,v=vcr},{p=pcr,ppri=0,psec=0}),{a,b,R});

b) Calcular a, b y vcr en función de Tcr, pcr y R. Esto es mejor porque así la R corresponde a la de los gases ideales y porque la vcr tiene gran incertidumbre experimental.

>	sol11:=solve(subs({T=Tcr,v=vcr},{p=pcr,ppri=0,psec=0}),{a,b,vcr});

c) Expresión del factor de compresibilidad en función de las magnitudes reducidas.

>	eqDefTR:=TR=T/Tcr;eqDefpR:=pR='p'/pcr;eqDefvR:=vR=v/vcr;Zcr:='pcr*vcr/(R*Tcr)';Zcr_:=subs(sol1,Zcr);Zcr__:=evalf(Zcr_,2);

d) Expresar la presión reducida en función de las otras magnitudes reducidas.

>	Z_:=collect(subs(T=TR*Tcr,p=pR*pcr,v=vR*vcr,sol1,Z),vcr);eqpR:=pR='(Z/Zcr)*TR/vR';pR:=expand((Z_/Zcr_)*TR/vR);#Z__:=convert(map(simplify,{op(Z_)}),whattype(Z_));

Sólo para la de van der Waals.

>	eqvR:=vR='(Z__/Zcr_)*TR/pR__';eqvR;eqZ3:=simplify(Z__*(vR-1/3)*vR=Z_*(vR-1/3)*vR);eqZ3:=expand(subs(eqvR,0=lhs(eqZ3)-rhs(eqZ3)));eqZ3_:=expand(eqZ3/coeff(rhs(eqZ3),Z__,3));

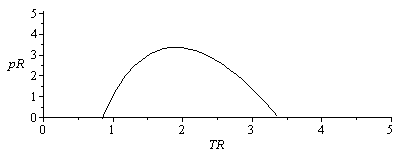
>	plot({seq(subs(TR=TR10/10,pR),TR10=6..15)},vR=0.34..3,'pR'=0..2,color=black);plot({seq(subs(TR=TR10/10,[pR,Z_,vR=0.34..10]),TR10=6..15)},'pR'=0..2,'Z'=0..1.1,color=black);

e)Puntos en los que las isotermas son horizontales en el diagrama Z-p y temperatura de Boyle, y comparación con la del diagrama generalizado de compresibilidad.

>	eqDef_TB:=Diff('Z','pR')[TR]=0;Diff('Z','pR')[TR]=Diff('Z',vR)[TR]/Diff('pR',vR)[TR];eqDef_TB:=Diff('Z',vR)[TR]=0;Diff('Z',vR)=diff(Z_,vR);TB_vR:=expand(solve(diff(Z_,vR)=0,TR));TB:=convert(asympt(TB_vR,vR,1),polynom);'TB'=evalf(TB,2);

La del diagrama generalizado de compresibilidad es aprox TR=2,5.

El lugar geométrico de los mínimos es:

>	Z_Tmin:=simplify(subs(TR=TB_vR,Z_));pR_Tmin:=simplify(subs(TR=TB_vR,pR));plot([pR_Tmin,Z_Tmin,vR=0.34..100],'pR'=0..5,'Z'=0..1.1,color=black);plot({seq(subs(TR=TR10/10,[(3/8)*vR*pR_Tmin/Z_Tmin,pR_Tmin,vR=0.34..100]),TR10=6..15)},'TR'=0..5,'pR'=0..5.1,color=black);

f) Curva de inversión y temperatura de inversión, y comparación con la del diagrama generalizado de compresibilidad.

>

eqJT:=mu=Diff(T,'p')[h];eqdh:=dh=c['p']*dT+(alpha*T-1)*v*dp;eqmu0:=T*Diff(v,T)['p']-v=0;eqmu0:=Diff('Z',TR)['pR']=0;eqmu0:=Diff('Z',TR)['vR']+Diff('Z',vR)['TR']*Diff(vR,TR)['pR']=0;dZ_dTR_vR:=diff(Z_,TR);dZ_dvR_TR:=diff(Z_,vR);dpR_dTR_vR:=diff(pR,TR);dpR_dvR_TR:=diff(pR,vR);dvR_dTR_pR:='-dpR_dTR_vR/dpR_dvR_TR';eqmu0:='dZ_dTR_vR+dZ_dvR_TR*dvR_dTR_pR=0';TI_vR:=solve(expand(eqmu0),TR);nsol:=nops([TI_vR]);if nsol>1 then TI_vR_:=TI_vR[nsol] else TI_vR_:=TI_vR fi; TI:=subs(rho=0,expand(subs(vR=1/rho,TI_vR_)));TI_:=evalf(TI,2);

En el diagrama de correcciones de h se atisba TI=5.

La curva de inversión, en paramétricas, será:

>	pR_TI:=subs(TR=TI_vR_,pR);

>	plot([TI_vR_,pR_TI,vR=.334..100],Temp=0..TI_,pres=0..20,numpoints=1000);

que se ajusta bien a los datos experimentales, que muestran que la temperatura de inversión (máxima) reducida está en torno a TRinv=6 (4..8), con el máximo de la curva para pRinv=12 (11..13) en torno a TR=2.5 (2..3). (Abajo puede verse la curva de inversión para el CO2)

La aproximación lineal es:

>	pR_TI_lin:=convert(series(subs(vR=1/rho,pR_TI),rho,2),polynom);TI_vR_lin:=convert(series(subs(vR=1/rho,TI_vR_),rho,2),polynom);pR_TI_lin:=subs(rho=solve(TI_vR_lin=TR_lin,rho),pR_TI_lin);

Respecto a las constantes a y b, la T de inversión es:

>	eqmu:=mu[JT]=(T*(-Diff(p,T)/Diff(p,v))-v)/cp;eqmu:=value(eqmu);eqmu0_lin:=0=expand(convert(series(subs(v=1/rho,rhs(eqmu)),rho,4),polynom));TI_:=solve(%,T);

Respecto a las constantes a y b, la te de Boyle es:

>	eqDef_TB:=Diff('Z','p')[T]=0;'Z'=rhs(eq1);dZ_dv_T:=diff(rhs(eq1),v);dp_dv_T:=diff(p,v);eqTB:=dZ_dv_T/dp_dv_T=0;TB_:=expand(solve(%,T));'TB'=2*'TI';

g) Repetir el problema para otras ecuaciones de estado:Dietericci, Redlich-Kwong,

Basta cambiar el dato al principio (eq1)

>

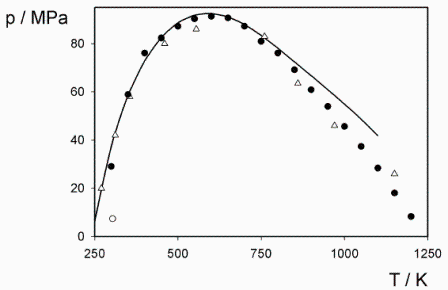
Fig. Curva de inversión para el dióxido de carbono.