>	restart:#"m04_p02":

Se pretende describir el comportamiento termodinámico de cierto líquido mediante las ecuaciones de estado: v(T,p)=a1+a2*T+a3/T+a4*T/p+a5*p/T   y   u(T,p)=b1+b2*T+b3/T+b4*T/p+b5*p/T;

siendo a1..b5 constantes a determinar experimentalmente. Se pide:

a) Determinar para qué valores de las constantes puede ser válido el modelo (téngase en cuenta que para p=0 se recupera el modelo de gas ideal).

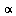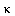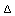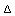b) Calcular cp, , , h y s en función de T y p.

c) Calcular la temperatura máxima que alcanzaría el gas al llenarse con él desde las condiciones ambientes (T0,p0) una botella donde previamente se ha hecho el vacío.

Datos

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(a1>0,a5>0,b2>0,b3>0,R>0,T>0,T0>0,T1>0,T2>0,p0>0,p1>0,p2>0,cv>0):

>	dat:=[v(T,p)=a1+a2*T+a3/T+a4*T/p+a5*p/T,u(T,p)=b1+b2*T+b3/T+b4*T/p+b5*p/T];

a) Determinar para qué valores de las constantes puede ser válido el modelo (téngase en cuenta que para p=0 se recupera el modelo de gas ideal).

>	eq1:=Diff(v,T)[p]=eval(subs(dat,diff(v(T,p),T)));eq2:=Diff(v,p)[T]=eval(subs(dat,diff(v(T,p),p)));eq3:=Diff(u,T)[p]=eval(subs(dat,diff(u(T,p),T)));eq4:=Diff(u,p)[T]=eval(subs(dat,diff(u(T,p),p)));

>	eqMaxw:=-Diff(s,p)[T]=Diff(v,T)[p];ds:=(du+p*dv)/T;eq5:=-Diff(s,p)[T]=(subs(eq2,eq4,(-Diff(u,p)[T]+p*(-Diff(v,p)[T]))/T)):eq5;

>	eqMaxw_:=simplify(subs(eq5,eq1,eqMaxw),T):eqMaxw_;ecua:=simplify(lhs(eqMaxw_))-simplify(rhs(eqMaxw_))=0:ecua;expand(ecua);

>	sol0:=[a2=0,a3=b5,b4=0];subs(sol0,dat);a4:=R;

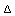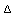b) Calcular cp, a, kh y s en función de T y p.

>	c[p]:=T*Diff(s,T)[p];c[p]:=Diff(u,T)[p]+p*Diff(v,T)[p];c[p]:=expand(eval(subs(eq1,eq3,dat,sol0,c[p])));

>	alpha:=(1/v)*Diff(v,T)[p];alpha:=factor(collect(expand(eval(subs(eq1,v=v(T,p),dat,sol0,alpha))),T));kappa:=(-1/v)*Diff(v,p)[T];kappa:=factor(collect(expand(eval(subs(eq2,v=v(T,p),dat,sol0,kappa))),p));

>	Z:=p*v(T,p)/(R*T);Z:=collect(expand(subs(dat,sol0,Z)),p);

>	dh:='c[p]*dT-(1-alpha*T)*v*dp';dh_:=collect(simplify(subs(v=v(T,p),dat,sol0,dh)),{dT,dp});Dh:=Int('dh[p=0]',T=T1..T2)+Int('dh[T=T2]',p=0..p2)-Int('dh[T=T1]',p=0..p1);Dh:=simplify(int(subs(p=0,dp=0,dh_)/dT,T=T1..T2)+int(subs(T=T2,dT=0,dh_)/dp,p=0..p2)-int(subs(T=T1,dT=0,dh_)/dp,p=0..p1));

>

ds:='c[p]/T*dT-alpha*v*dp';ds_:=collect(expand(simplify(subs(v=v(T,p),dat,sol0,ds))),{dp,dT});Ds:=Int('ds[p=0]',T=T1..T2)+Int('ds[T=T2]',p=0..p2)-Int('ds[T=T1]',p=0..p1);Ds:=collect(expand(int(subs(dp=0,p=0,ds_)/dT,T=T1..T2)+int(subs(T=T2,dT=0,ds_)/dp,p=0..p2)-int(subs(T=T1,dT=0,ds_)/dp,p=0..p1)),{R,b2,b3});

>

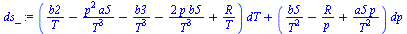c) Calcular la temperatura máxima que alcanzaría el gas al llenarse con él desde las condiciones ambientes (T0,p0) una botella donde previamente se ha hecho el vacío.

>	eqBE:=D(mu)=h[0]*Dm;eqBE:=u-u[0]=h[0]-u[0];eqBE:=u-u[0]=p0*v0;eqBE:=h-h[0]-p*v+p0*v0=p0*v0;eqBE:=h-h[0]=p*v;eqBE:=subs(T1=T0,p1=p0,p2=p0,Dh)=subs(dat,sol0,p=p0,T=T2,p*v(T,p));T_:=expand(solve(eqBE,T2));

Comprobación en el límite de gas ideal: a1=0,a5=0,b3=0,b5=0.

>	LGI:=[a1=0,a5=0,b3=0,b5=0];'T_'=collect(convert(series(subs(a1=0,a5=0,b3=0,b5=0,T_),b2=0,2),polynom),T0);c[p,MGI]:=subs(LGI,c[p]);c[v]:='c[p]-alpha^2*T*v/kappa';c[v,MGI]:=subs(LGI,c[p]-alpha^2*T*subs(dat,sol0,v(T,p))/kappa);'T_'=simplify(expand(simplify(subs(LGI,b2=cv,R=cp-cv,cp=gamma*cv,T_))));

>