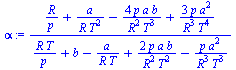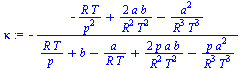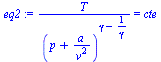>	restart:#"m04_p01"

Se pide:

a) Demostrar la relación de Mayer generalizada, cp-cv=vT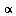^2/k, a partir de las definiciones de los coeficientes.

b) Desarrollar la expresión anterior para la ecuación de estado de van der Waals a presiones bajas.

c) ¿Qué expresión tendrían las relaciones isoentrópicas para un gas de van der Waals si se pudiera aproximar la relación de Mayer generalizada por cp-cv=R?

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	assume(p>0,a>0,v>0,b>0,R>0,T>0);eqET:=(p+a/v^2)*(v-b)=R*T;

a) Demostrar la relación de Mayer generalizada, cp-cv=vT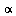^2/k, a partir de las definiciones de los coeficientes.

>	eq4_17_1;eq4_17_3;eq4_17_11:=ds=c[v]*dT/T+Diff(s,v)[T]*dv;

>	ds:=Diff(s,T)[p]*dT+Diff(s,p)[T]*dp;ds:=Diff(s,T)[v]*dT+Diff(s,v)[T]*dv;eq1:=Diff(s,T)[v]=Diff(s,T)[p]+Diff(s,p)[T]*Diff(p,T)[v];

>	eq11:=Diff(s,T)[v]=subs(eq4_17_11,dv=0,ds/dT);

>	eq12:=Diff(s,T)[p]=subs(eq4_17_1,dp=0,ds/dT);

>	eq13:=Diff(s,p)[T]=subs(eq4_17_1,dT=0,ds/dp);

>	eq14:=Diff(p,T)[v]=subs(dp=solve(eq4_17_3,dp),dv=0,dp/dT);

>	eq1_:=subs(eq11,eq12,eq13,eq14,eq1);c[p]=expand(solve(eq1_,c[p]));

b) Desarrollar la expresión anterior para la ecuación de estado de van der Waals a presiones bajas.

>	eqET;v_:=solve(expand(eqET),v):'v_[1]'=v_[1]:num_sol:=nops([v_]);

>	v1:=expand(simplify(expand(convert(series(p*v_[1],p=0,3),polynom)))/p);alpha:=(1/v1)*diff(v1,T);kappa:=(-1/v1)*diff(v1,p);cp_cv:=convert(series(v1*T*alpha^2/kappa,p=0,2),polynom);

c) ¿Qué expresión tendrían las relaciones isoentrópicas para un gas de van der Waals si se pudiera aproximar la relación de Mayer generalizada por cp-cv=R?

>	eqisent:=du+p*dv=0;eqsust_perf:=du=c[v]*dT;eqCp_Cv_R:=a=0;eqisent_:=c[v]*dT+R*T*dv/(v-b)=0;eq1:=T*(v-b)^(gamma-1)=cte;eq2:=T/(p)^((gamma-1/gamma))=cte;eq2:=T/(p+a/v^2)^((gamma-1/gamma))=cte;eq3:=p*(v-b)^gamma=cte;eq3:=(p+a/v^2)*(v-b)^gamma=cte;

>