>	restart:#"m03_p23"

Considérese un cilindro horizontal de 15 cm de diámetro y 75 cm de longitud, cerrado por ambos extremos, con un émbolo cilíndrico de 2 kg de acero, cuyo centro está inicialmente a ¼ de la longitud del cilindro, separando dos masas de aire. La presión y la temperatura iniciales del conjunto son las del ambiente, que está a 20 ºC y 94 kPa. En una primera etapa se fuerza el desplazamiento del émbolo, lentamente, hasta la posición central del cilindro, y a partir de ahí se suelta. Se pide:

a) Estimar el efecto del espesor del émbolo y calcular el trabajo necesario para desplazar el émbolo.

b) Flujos de energía en el proceso anterior, para cada masa de aire.

c) Estado de equilibrio mecánico tras la suelta (antes del atemperamiento).

d) Flujos de energía en el proceso anterior, para cada masa de aire.

e) Calor intercambiado con el ambiente y generación de entropía en el proceso global.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):assume(LE>0,x1>LE,x2>x1,x2<L-LE/2,x1>L-LE/2,L>x2):

>	su1:="Aire":su2:="Acero":dat:=[D=0.15*m_,L=0.75*m_,mE=2e*kg_,x1=(0.75/4)*m_,T0=(20+273.15)*K_,p0=94e3*Pa_,x2=(0.75/2)*m_];

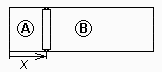
Esquema:

>

>

Ecs. const.:

>	Adat:=get_gas_data(su1):Sdat:=get_sol_data(su2):dat:=op(dat),Const,SI2,SI1:rhoE:=subs(Sdat,rho);

a) Estimar el efecto del espesor del émbolo y calcular el trabajo necesario para desplazar el émbolo.

Veamos si es relevante el espesor del émbolo.

>	eqLE:=LE=mE/(rho*A);eqA:=A=Pi*D^2/4;eqA_:=evalf(subs(dat,%));eqLE_:=subs(eqA_,rho=rhoE,dat,eqLE);LE:=0;

Puede despreciarse si se admiten incertidumbres de 2*LE/L=2*0,01/0,75=4%.

El trabajo que hay que hacer (por medio de un dispositivo no descrito, e.g. un imán) es para vencer las diferencias de presión que van surgiendo. El proceso será isotermo (muy lento).

>

W12:=Int((pB-pA)*A,x=x1..x2);p=m*R*T/V;VA:=(x-LE/2)*A;VB:=(L-x-LE/2)*A;eqmA:=mA=subs(x=x1,eqLE_,p0*VA/(R*T0));eqmA_:=subs(dat,subs(Adat,eqA_,dat,%));eqmB:=mB=subs(x=x1,eqLE_,p0*VB/(R*T0));eqmB_:=subs(dat,subs(Adat,eqA_,dat,%));W12:=Int((mB*R*T0/VB-mA*R*T0/VA)*A,x=x1..x2);W12_:=-mB*R*T0*ln((L-x2-LE/2)/(L-x1-LE/2))-mA*R*T0*ln((x2-LE/2)/(x1-LE/2));W12__:=subs(dat,evalf(subs(eqmA_,eqmB_,eqLE_,eqA,Adat,dat,W12_)));pA1=p0;pB1=p0;eqpA2:=pA2=mA*R*T0/subs(x=x2,VA);eqpB2:=pB2=mB*R*T0/subs(x=x2,VB);eqpA2_:=subs(dat,subs(eqLE_,eqA_,eqmA_,Adat,dat,eqpA2));eqpB2_:=subs(eqLE_,eqmB,eqA_,Adat,dat,eqpB2);

i.e. hay que aportar unos 167 J (163 J si se toma LE=0); i.e. unos 170 J.

b) Flujos de energía en el proceso anterior, para cada masa de aire.

De 1 a 2 es isotermo, Q=-W, con p=mRT0/V.

>

eqBE:=DE=W+Q;QA12=-WA12;QA12=Int(pA*A,x=x1..x2);QA12_:=mA*R*T0*ln((x2-LE/2)/(x1-LE/2));QA12__:=subs(dat,evalf(subs(eqA_,eqLE_,eqmA_,Adat,dat,%)));QB12=-WB12;QB12=Int(-pB*A,x=x1..x2);QB12_:=mB*R*T0*ln((L-x2-LE/2)/(L-x1-LE/2));QB12__:=subs(dat,evalf(subs(eqA_,eqLE_,eqmB_,Adat,dat,%)));QA12+QB12=QA12__+QB12__;

i.e., de 1 a 2, el A toma 213 J de calor del ambiente y cede 213 J de trabajo al émbolo, mientras que el B cede 380 J de calor al ambiente y recibe 380 J de trabajo del émbolo. En conjunto, de 1 a 2 salen 167 J de calor, igual al trabajo neto aportado.

c) Estado de equilibrio mecánico tras la suelta (antes del atemperamiento).

>	eqEqMec:=pA3=pB3;p3*V3^gamma=p2*V2^gamma;eqEqMec:=pA2*((x2-LE/2)/(x3-LE/2))^gamma=pB2*((L-x2-LE/2)/(L-x3-LE/2))^gamma;eqEqMec_:=pA2^(1/gamma)*((x2-LE/2)/(x3-LE/2))=pB2^(1/gamma)*((L-x2-LE/2)/(L-x3-LE/2));x3_:=solve(subs(eqLE_,eqpA2_,eqpB2_,Adat,eqA_,dat,%),x3);

i.e. el centro del émbolo queda a 0,235 m (entre la posición inicial, x1=0,188 m, y la intermedia, x2=0,375 m).

d) Flujos de energía en el proceso anterior, para cada masa de aire.

De 2 a 3 cada gas evoluciona adiabáticamente, Q=0, y, aunque la fricción disipe calor al émbolo y al cilindro, no habrá tiempo de que llegue al ambiente, luego también para el conjunto A+B+C+E será Q=0.

>	eqBE:=DE=W+Q;eqBE:=DE=W;DE:=m*c[v]*(T3-T2);DE:=m*c[v]*T0*(T3/T2-1);DEA:=mA*c[v]*T0*((x2/x3)^(gamma-1)-1);DEB:=mB*c[v]*T0*(((L-x2)/(L-x3))^(gamma-1)-1);DEA23_:=subs(eqmA,x3=x3_,Adat,eqA_,dat,DEA);DEB23_:=subs(eqmB,x3=x3_,Adat,eqA_,dat,DEB);

i.e. el gas A recibe un trabajo de 154 J del émbolo, mientras que el gas B ha dado 275 J de trabajo; como el émbolo ya está parado, la diferencia es el trabajo disipado por fricción: 275-154=121 J.

d) Calor intercambiado con el ambiente y generación de entropía en el proceso global.

De 3 a 4 todo se atemperará, y como el proceso global es cíclico (el sistema vuelve a su estado inicial), 0=DE=Q+W=Q12+Q23+Q34+W12+W23+W34=Q12+Q34+W12, ya que para el conjunto W34=0, luego ha de ser también Q34=0.  

Para el sistema conjunto, A+B+C+E, en el proceso global, 1-2-3-4, será Q=-W.

El universo, conjunto más ambiente, es un sistema aislado. Además, el conjunto sufre una evolución cíclica, luego:

>	eqBE:=0=W1234+Q1234;W1234='W12';Q1234_:=-W12__;Q34:=Q1234-(QA12+QB12);Q34_:=Q1234_-(QA12__+QB12__);Sgen:=DS-Int(1/T,Q);Sgen:=DSconj+DSamb;Sgen:=DSamb;Sgen:=Qamb/Tamb;Sgen:=-(Q1234/T0);Sgen_:=subs(dat,-Q1234_/T0);

i.e. se generan 0,6 J/K.

>