>	restart:#"m03_p21"

En una publicación se dice que una máquina de refrigeración por absorción, MA, alcanza una eficiencia energética ≡QC/QH=40% en la producción de frío a TC=9 ºC a partir de calor a TH=55 ºC, en un ambiente a T0=28 ºC. Se pide:
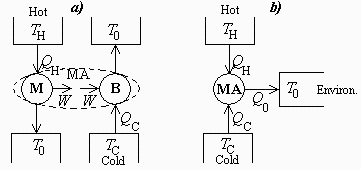
a) Esquema de bloques de las fuentes térmicas y los flujos de energía intercambiados con la máquina de refrigeración.
b) Balance de energía del conjunto.
c) Balance de entropía del conjunto.
d) Balance de exergía del conjunto.
e) Determinar si los datos son incompatibles.
f) Calcular la eficiencia energética máxima para esas temperaturas.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	dat:=[eta=0.4,TC=(9+273)*K_,TH=(55+273)*K_,T0=(28+273)*K_];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Esquema de bloques de las fuentes térmicas y los flujos de energía intercambiados con la máquina de refrigeración.

(Ver figura.)

La máquina de absorción, MA, puede representarse por la combinación de dos máquinas simples como se esquematiza en a) (una máquina de motor térmico, M, y de una máquina de bombeo térmico, B), o directamente como una máquina combinada, MA,  como se esquematiza en b).

Se trata de un problema de fuentes térmicas, no siendo necesario conocer ningún detalle de las posibles sustancias de trabajo y procesos a realizar en una máquina de absorción particular.

b) Balance de energía del conjunto.

Si elegimos como sistema todo (i.e. el universo termodinámico), se trata de un sistema aislado (Univ=MA+H+C+Environ.).

En régimen estacionario, DE(MA)=0, pero no las fuentes, que no pueden estar en régimen estacionario porque sólo dan (o toman).

>	eqBE:=DE=0;eqBE:=DE_MA+DE_H+DE_C+DE_0=0;eqBE:=0-QH-QC+Q0=0;

c) Balance de entropía del conjunto.

Sistema aislado (Univ=MA+H+C+Environ.)..En régimen estacionario, DS(MA)=0, pero el de las fuentes es Qi/Ti.

>	eqBS:=DS>=0;eqBS:=DS_MA+DS_H+DS_C+DS_0>=0;eqBS:=0-QH/TH-QC/TC+Q0/T0>=0;

d) Balance de exergía del conjunto.

Sistema aislado (Univ=MA+H+C+Environ.)..En régimen estacionario, DPhi(MA)=0, pero el de las fuentes es Qi*(1-T0/Ti), i.e. la exergía de una cantidad de calor Q a una temperatura T respecto a un ambiente a T0 es Qi*(1-T0/Ti).

>	eqBX:=DPhi<=0;eqBX:=QH*(1-T0/TH)+QC*(1-T0/TC)>=0;eqBX_:='eqBE-T0*eqBS';eqBX_:=collect(expand(lhs(eqBE)-T0*rhs(eqBS)<=0),[QH,QC]);

Puede comprobarse que el balance exergético es combinación del energético y entrópico.

e) Determinar si los datos son incompatibles.

f) Calcular la eficiencia energética máxima para esas temperaturas.

>	eqeta:=eta=QC/QH;eqDat:=subs(dat,%);eqBX;eqBXlim:=0=rhs(eqBX);eta_max:=QC/solve(eqBXlim,QH);eta_max_:=evalf(subs(dat,eta_max));

El límite termodinámico es una eficiencia energética de 1,22 y el dato es 0,4, luego, no es incompatible con las leyes de la termodinámica; en principio sí es posible que una máquina real funcione con este rendimiento (las necesarias irreversibilidades de la máquina real serán responsables del decremento de eficiencia).

NOTA. Este problema puede resolverse tomando como sistema la máquina de absorción, MA, en lugar del universo, así:

Ahora el sistema (MA) es un sistema cerrado en régimen estacionario.

b) Balance de energía del conjunto.

En régimen estacionario, el balance energético de la máquina, DE=Q+W, queda 0=SumQi+0.

>	eqBE:=DE=Q+W;eqBE:=0=QH+QC-Q0+0;

c) Balance de entropía del conjunto.

En régimen estacionario, el balance energético de la máquina, DS=Q/T+Sgen queda 0=SumQi/Ti+Sgen, con Sgen>=0, i.e. SumQi/Ti<=0.

>	eqBS:=DS=Q/T+Sgen;eqBS:=0=QH/TH+QC/TC-Q0/T0+Sgen;eqBS_:=QH/TH+QC/TC-Q0/T0<=0;

d) Balance de exergía del conjunto.

En régimen estacionario, el balance energético de la máquina, DPhi=Wu+SumQi*(1-T0/Ti)+Int(dQ(1-T0/T)-T0Sgen, se reduce a 0=0+SumQi*(1-T0/Ti)-degradación, i.e. SumQi*(1-T0/Ti)>=0.

>	eqBX:=DPhi=Wu+Qi*(1-T0/Ti)+Int(1-T0/T,Q)-T0*Sgen;eqBX:=0=0+QH*(1-T0/TH)+QC*(1-T0/TC)+Int(1-T0/T,Q)-T0*Sgen;eqBX_:=QH*(1-T0/TH)+QC*(1-T0/TC)>=0;

Puede comprobarse que el balance exergético es combinación del energético y entrópico.

e) Determinar si los datos son incompatibles.

f) Calcular la eficiencia energética máxima para esas temperaturas.

>	eqeta:=eta=QC/QH;eqDat:=subs(dat,%);eqBX_;eqBXlim:=0=rhs(eqBX_);eta_max:=QC/solve(eqBXlim,QH);eta_max_:=evalf(subs(dat,eta_max));

Obteniéndose el mismo resultado.

>