>	restart:#"m03p20"

Para la calefacción de un cierto edificio, se ha calculado que se necesita 1 MW de potencia térmica. La instalación va a ser de radiadores de agua caliente, y se quieren comparar diferentes alternativas para calentar el agua desde 15 ºC hasta 95 ºC. Se pide:
a) Determinar el flujo de agua a calentar, e indicar por qué no conviene calentarla eléctricamente.
b) Suponiendo que se va a usar una caldera de gas natural que aprovecha el 90 % del poder calorífico del combustible, determinar la energía del combustible necesario por unidad de tiempo, y el incremento de entropía del agua por unidad de tiempo al pasar por la caldera.
c) Suponiendo que, en lugar de la caldera, se fuera a usar un motor térmico de gas natural con un rendimiento energético del 40%, determinar la potencia eléctrica que se generaría si se dimensionara el motor para que el calor evacuado fuera igual a la demanda de calefacción del edificio.
d) Supóngase ahora que el agua se calentara con una bomba de calor de rendimiento 50% del máximo de Carnot, movida por un motor térmico de 40% de rendimiento; calcular la relación de consumos de combustible respecto a la caldera.
e) Supóngase por último que en la configuración del apartado anterior, se aprovecha también el calor evacuado del motor para calentar el agua, y calcúlese la relación de consumos de combustible respecto a la caldera.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="H2O":dat:=[Qdot=1e6*W_,T1=(15+273)*K_,T2=(95+273)*K_,eta[cal]=0.9,eta[mot]=0.4,eta[bom]=0.5*eta[BCarnot]];

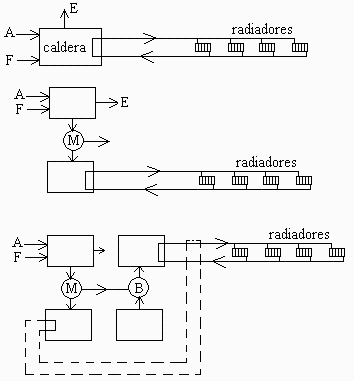
Esquema:

Eqs. const.:

>	dat:=op(dat),get_liq_data(su),Const,SI2,SI1:

a) Determinar el flujo de agua a calentar, e indicar por qué no conviene calentarla eléctricamente.

>	eqBE:=Qdot=mdot*c*(T2-T1);mdot_:=subs(dat,solve(%,mdot));

i.e. hay que calentar 3 kg/s de agua, lo cual se suele hacer en una caldera quemando un combustible, porque con resistencias eléctricas es prohibitivo el gasto de operación, ya que el precio de la energía eléctrica suele ser el doble o el triple del de la misma energía de combustión (la mayoría de la electricidad se produce por combustión con un rendimiento menor del 40%), aunque la instalación inicial costaría menos. (Aparte de esto, se necesitaría una acometida eléctrica de alto voltaje, pero este problema es similar al del gas, ya que si el consumo es muy grande se necesita suministrarlo a mayor presión).

b) Suponiendo que se va a usar una caldera de gas natural que aprovecha el 90 % del poder calorífico del combustible, determinar la energía del combustible necesario, y el incremento de entropía del agua al pasar por la caldera.

>	eqBE:=Qcald=Qdot/eta[cal];eqBE_:=subs(dat,%);eqBS:=DS=Int(1/T,Q)+S[gen]+Sum(Int(s[e],m[e]),i=1..Abert);eqDSdot:=DSdot=mdot*(s2-s1);eqDSdot:=DSdot=mdot*c*ln(T2/T1);eqDSdot_:=evalf(subs(mdot=mdot_,dat,%));

i.e. se consumiría un consumo de gas equivalente a 1,1 MW, y los 3 kg/s de agua sufren un incremento de entropía de 3 kW/K, en total, o de 1020 J/(kg·K) por cada kg/s de flujo.

c) Suponiendo que, en lugar de la caldera, se fuera a usar un motor térmico de gas natural con un rendimiento energético del 40%, determinar la potencia eléctrica que se generaría si se dimensionara el motor para que el calor evacuado fuera igual a la demanda de calefacción del edificio.

>	eqBE:=Qmot_in=Wmot+Qmot_out;eqetamot:=eta[mot]=Wmot/Qmot_in;eqQout:=Qmot_out=Qdot;eqQout_:=subs(dat,%);eqs:=subs(%,dat,solve({eqBE,eqetamot},{Wmot,Qmot_in}));

i.e. se generarían 0,67 MW de electricidad además de 1 MW para la calefacción, necesitándose más gas: el equivalente a 1,7 MW.

Hay que hacer notar que no todo el calor residual sería recuperable en la práctica (exigiría camboiadores de calor infinitamente grandes), pero la diferencia no es fundamental.

d) Supóngase ahora que el agua se calentara con una bomba de calor de rendimiento 50% del máximo de Carnot, movida por un motor térmico de 40% de rendimiento; calcular la relación de consumos de combustible respecto a la caldera.

>

eqBEmot:=eqBE;eqetamot;eqBEbom:=Qbom_out=Wbom+Qbom_in;eqBEmotbom:=Wmot=Wbom;eqetabom:=eta[bom]=Qbom_out/Wbom;eqetaCarnot:=eta[BCarnot]=T2/(T2-T1);eqetaCarnot_:=evalf(subs(dat,%));eqQout:=Qdot=Qbom_out;eqs:=solve(subs(eqBEmotbom,dat,eqetaCarnot_,dat,{eqBEmot,eqBEbom,eqQout,eqetamot,eqetabom}),{Wbom,Qbom_in,Qbom_out,Qmot_in,Qmot_out});Qmot_in=subs(eqs,Qmot_in);eqBE_;eqBEmotbom_cald=subs(eqBE_,eqs,Qmot_in/Qcald);

i.e. ahora el conjunto consumiría 1,1 MW de combustible, casi lo mismo que la caldera (98%), y ya no generaría electricidad, por lo que se ve claramente que es mejor la solución de la caldera (cuesta mucho menos y consume sólo un 2% más).

e) Supóngase por último que en la configuración del apartado anterior, se aprovecha también el calor evacuado del motor para calentar el agua, y calcúlese la relación de consumos de combustible respecto a la caldera.

>

eqBEmot:=eqBE;eqetamot;eqBEbom:=Qbom_out=Wbom+Qbom_in;eqBEmotbom:=Wmot=Wbom;eqetabom:=eta[bom]=Qbom_out/Wbom;eqetaCarnot:=eta[BCarnot]=T2/(T2-T1);eqetaCarnot_:=evalf(subs(dat,%));eqQout:=Qdot=Qmot_out+Qbom_out;eqs:=solve(subs(eqBEmotbom,dat,eqetaCarnot_,dat,{eqBEmot,eqBEbom,eqQout,eqetamot,eqetabom}),{Wbom,Qbom_in,Qbom_out,Qmot_in,Qmot_out});Qmot_in=subs(eqs,Qmot_in);eqBE_;eqBEmotbom_cald=subs(eqBE_,eqs,Qmot_in/Qcald);

i.e. basta consumir un equivalente en gas de 0,66 MW en el motor, que generaría 0,34 MW para mover la bomba, y el 1 MW de calefacción se satisfaría, idealmente, con 0,61 MW de aporte de la bomba más 0,39 MW de calor de escape del motor.

Esta solución "motor térmico más bomba de calor" sólo consumiría un 59% del combustible necesario usando una caldera, aunque sería mucho más cara de instalar y mantener. Habría que hacer un estudio termo-económico para ver si es rentable la inversión (suele ser rentable si la diferencia de coste de instalación se amortiza en unos 5 años por el ahorro de combustible, pero depende de la fiabilidad de los equipos, de los suministradores, del equipo de mantenimiento, de los incentivos fiscales, la incertidumbre económica y el riesgo asumible...).

>