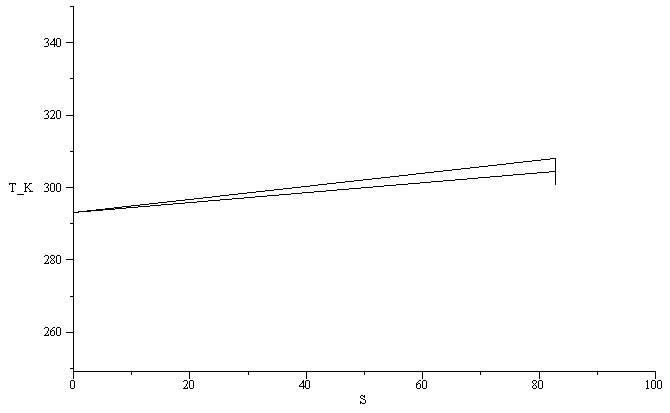>	restart:#"m02_p11"

En un cilindro abierto por arriba, un émbolo de latón de 11 cm de diámetro y 2 cm de espesor, encierra 0,1 mol de metano inicialmente en equilibrio, en un ambiente a 20 ºC y 94 kPa. A partir de un cierto instante se eleva la temperatura a volumen constante hasta alcanzar una sobrepresión adicional equivalente a 500 mm de columna de agua y después se deja libre el émbolo. Se pide:

a) Presión y altura inicial.
b) Presión y temperatura tras el calentamiento.
c) Presión, altura y temperatura tras el equilibrio mecánico.
d) Presión, altura y temperatura tras el equilibrio térmico total.
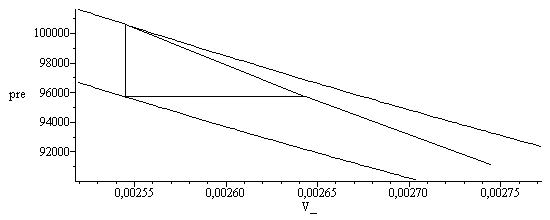
e) Representación de la evolución en los diagramas p-V y T-s.

f) Altura máxima y periodo del movimiento del émbolo (tras la suelta) en el límite de baja fricción.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="CH4":su2:="Laton":su3:="H2O":dat:=[A=evalf(Pi*(0.11*m_)^2/4),e=0.02*m_,n=0.1*mol_,T0=(20+273)*K_,Dp12mmca=0.5*m_,p0=94e3*Pa_]:'dat'=evalf(%,3);

Esquema:

>

>

Ecs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su1):sdat:=get_sol_data(su2):ldat:=get_liq_data(su3):rho[laton]:=subs(sdat,rho);dat:=op(dat),Const,gdat,ldat,SI2,SI1:gamma=evalf(subs(dat,gamma),3);

a) Presión y altura inicial

>

eqBF:=mE*diff(z(t),t,t)=(p-p0)*A-mE*g-Ff;eqBFint:=int(mE*diff(z(t),t,t)*diff(z(t),t),t)=Int((p-p0)*A-mE*g-Ff,z);T1:=T0:m:=n*M;masa_:=subs(dat,m);p1:=p0+DpE;DpE_:=rho*g*e;DpE__:=subs(rho=rho[laton],dat,DpE_):'DpE'=evalf(%/(1000*Pa_/kPa_),2);p1_:=subs(DpE=DpE__,dat,p1):'p1'=evalf(%/(1000*Pa_/kPa_),3);V1:=solve(subs(p=p1,T=T1,eqET),V);V1_:=subs(DpE=DpE__,dat,V1):'V1'=evalf(%,2);z1_:=subs(dat,V1_/A):'z1'=evalf(%,3);mE_:=subs(dat,rho[laton]*A*e):'mE'=evalf(%,2);

b) Presión y temperatura tras el calentamiento.

>	V2:=V1:Dp12:=rho*g*Dp12mmca;Dp12_:=subs(dat,Dp12):'Dp12'=evalf(%/(1000*Pa_/kPa_),2);p2:='p1+Dp12';p2_:=p1_+Dp12_:'p2'=evalf(p2_/(1000*Pa_/kPa_),4);T2:='T1*p2/p1';T2_:=subs(rho=rho[laton],p2=p2_,dat,T0*p2_/p1_);V2_:=V1_:'V2'='V1';z2_:=z1_:'z2'='z1';

c) Presión, altura y temperatura tras el equilibrio mecánico.

>	p3:='p1';p3_:=p1_:'p3'=evalf(p1_/(1000*Pa_/kPa_),3);T3:='T2*(p3/p2)^((gamma-1)/gamma)';T3_:=subs(dat,T2_*(p3_/p2_)^((gamma-1)/gamma));V3_:=solve(subs(p=p3_,T=T3_,dat,eqET),V):'V3'=evalf(V3_,2);z3_:=subs(dat,V3_/A):'z3'=evalf(%,3);

d) Presión, altura y temperatura tras el equilibrio térmico total.

>	p5:=p1;p5_:=p1_:'p5'=evalf(p1_/(1000*Pa_/kPa_),3);T5:=T1;V5:='V1';V5_:=V1_:'V5'=evalf(%,2);z5_:=z1_:'z5'=evalf(%,3);

e) Representación de la evolución en los diagramas p-V y T-s.

f) Altura mínima y periodo del movimiento del émbolo (tras la suelta) en el límite de baja fricción.

>

eqBE24:=0=rhs(eqBFint);eqBE24:='m*c[v]*(T4-T2)=-p1*A*(z4-z2)';eqBE34_:=subs(T4=T2_*(z2_/z4)^(gamma-1),dat,SI0,n*M*c[v]*(T4-T2_)=-p1_*A*(z4-z2_));z4_:=fsolve(eqBE34_,z4=(z2_/m_+1e-3)..2*z2_/m_)*m_:'z4'=evalf(%,3);T4_:=subs(dat,T2_*(z2_/z4_)^(gamma-1));V4_:=subs(dat,z4_*A):'V4'=evalf(%,2);p4_:=subs(dat,n*R[u]*T4_/V4_):'p4'=evalf(%/(1000*Pa_/kPa_),3);

>

plot({[[V1_/m_^3,p1_/Pa_],[V2_/m_^3,p2_/Pa_]],[[V2_/m_^3,p2_/Pa_],[V3_/m_^3,p3_/Pa_]],[[V3_/m_^3,p3_/Pa_],[V4_/m_^3,p4_/Pa_]],[[V3_/m_^3,p3_/Pa_],[V5_/m_^3,p5_/Pa_]],p1_/Pa_*(V1_/m_^3/V_),p2_/Pa_*(V2_/m_^3/V_),0*p2_/Pa_*(V2_/m_^3/V_)^subs(dat,gamma)},V_=0.99*V2_/m_^3..1.01*V4_/m_^3,pre=0.99*p4_/Pa_..1.01*p2_/Pa_,colour=black);

>

DS12:=c[p]*ln(T2_/T1)-R*ln(p2_/p1_):DS23:=c[p]*ln(T3_/T2_)-R*ln(p3_/p2_):DS34:=c[p]*ln(T4_/T3_)-R*ln(p4_/p3_):DS45:=c[p]*ln(T5/T4_)-R*ln(p5_/p4_):DS1_2_3_4_5:=evalf(subs(dat,SI0,[DS12,DS23,DS34,DS45])):'DS1_2_3_4_5'=evalf(%,2);S0:=0:plot(subs(dat,SI0,[[S0,T1],[S0+DS12,T2_],[S0+DS12+DS23+DS34,T4_],[S0+DS12+DS23,T3_],[S0+DS12+DS23+DS45,T5]]),'S'=0..100,T_K=250..350,colour=black);

>	omega:=sqrt(gamma*p1*A/(mE*z2));omega_:=subs(dat,SI0,sqrt(gamma*p1_*A/(mE_*z2_))):'omega'=evalf(%,2)/s_;Ti_:=evalf(subs(dat,SI0,2*Pi/omega_))*s_:'Ti'=evalf(%,2);

>
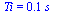