>	restart:#"m02_p10"

Un cilindro horizontal de 10 cm2 de sección y 40 cm de longitud está cerrado por un extremo. A 10 cm del fondo hay un tabique de pequeño espesor, con una válvula (a través de la cual se ha hecho el vacío) y una gran compuerta inicialmente cerrada. En el extremo abierto del cilindro se coloca un émbolo de 0,3 kg, de baja fricción, y en un momento dado se abre bruscamente la compuerta. Suponiendo que el aire encerrado alcanza el equilibrio interno antes de que el émbolo se haya desplazado apreciablemente, se pide:

a)  Hacer un esquema de la instalación propuesta y definir el estado inicial del gas encerrado (estado 0).

b)  Calcular el estado termodinámico tras la apertura, antes del movimiento del émbolo (estado 1).

c)  Calcular el estado termodinámico tras el equilibrado mecánico (estado 2).

d)  Calcular el estado termodinámico al cabo de mucho tiempo (estado 3).

e)  Hacer un esquema de la evolución en los diagramas p-V y T-s..

f)  Calcular el incremento de entropía en cada proceso.

g)  Determinar la posición más cercana al fondo que llegaría a alcanzar el émbolo.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Aire":dat:=[A=10e-4*m_^2,L=0.4*m_,Lv=0.1*m_,mE=0.3*kg_];

Esquema:

>

>

Ecs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su):dat:=op(dat),Const,gdat,SI2,SI1:

a)  Hacer un esquema de la instalación propuesta y definir el estado inicial del gas encerrado (estado 0).

>	V0:=A*(L-Lv);V0_:=subs(dat,V0);x0_:=subs(dat,L);m__:=subs(dat,p0*V0/(R*T0));dat:='m'=m__,dat:

i.e. hay 0,36 g de aire encerrado en un volumen de 0,30 L a 288 K y 100 kPa.

b)  Calcular el estado termodinámico tras la apertura, antes del movimiento del émbolo (estado 1).

DE=Q+W implica DE=0, luego T1=T0, y como V0=A*(L-Lv), V1=A*L, entonces p1=p0*V0/V1.

>	T1:=T0;V1:=A*L;p1:=p0*V0/V1;V1_:=subs(dat,A*L);x1_:=subs(dat,V1_/A);p1_:=subs(dat,p0*V0/V1_):'p1'=evalf(%/(1000*Pa_/kPa_));

i.e., ahora los 0,36 g de aire encerrado ocupan un volumen de 0,40 L a 288 K y 75 kPa.

c)  Calcular el estado termodinámico tras el equilibrado mecánico (estado 2).

>	p2:=p0;V2:=V1*(p1/p2)^(1/ga);p2_:=subs(dat,p0):V2_:=subs(dat,V1_*(p1_/p2_)^(1/gamma));x2_:=subs(dat,V2_/A):'x2'=evalf(%,2);T2_:=subs(dat,p2_*V2_/(m*R));

i.e., tras pararse el émbolo, pero antes de la transmisión de calor, los 0,36 g de aire ocupan 0,33 L y quedan a 100 kPa y 313 K, calentado por el trabajo que ha hecho la atmósfera.

d)  Calcular el estado termodinámico al cabo de mucho tiempo (estado 3).

Equilibrio final: T3=T0, p3=p0, luego x3=L-Lv.

>	T3:=T0;p3:=p0:x3:=m*R*T3/(p3*A);x3_:=subs(dat,m*R*T3/(p3*A));V3_:=subs(dat,x3_*A);

e)  Hacer un esquema de la evolución en los diagramas p-V y T-s..

Se ha incluido en el esquema la evolución isoentrópica más allá del equilibrio mecánico.

>

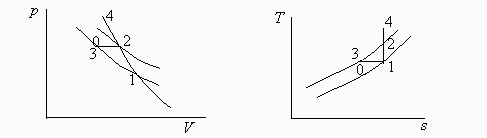
f)  Calcular el incremento de entropía en cada proceso.

>

Q01_:=0;W01_:=0;DE01_:=0;DS01air:='-m*R*ln(p1/p0)';DS01air_:=subs(dat,evalf(subs(dat,DS01air))):'DS01air'=evalf(%,2);DS01atm_:=0;Q12_:=0;W12_:=-Int('A*p1*(x1/x)^gamma',x=x1..x2);W12__:=subs(x1=x1_,x2=x2_,dat,SI0,value(W12_))*J_:'W12'=evalf(%,2);DE12_:=subs(dat,m*c[v]*(T2_-T1)):'DE12'=evalf(%,2);W12atm_:=subs(dat,p0*(V1_-V2_)):'W12atm'=evalf(%,2);W12fric_:=W12atm_-W12__:'W12fric'=evalf(%,2);DS12air_:=0;DS12atm_:=0;DE23_:=subs(dat,m*c[v]*(T3-T2_)):'DE23'=evalf(%,2);W23_:=subs(dat,p0*(V2_-V3_)):'W23'=evalf(%,2);Q23_:=DE23_-W23_:'Q23'=evalf(%,2);DS23air_:=subs(dat,evalf(subs(dat,m*c[p]*ln(T3/T2_)))):'DS23air'=evalf(%,2);DS23atm_:=subs(dat,-Q23_/T0):'DS23atm'=evalf(%,2);DE0123_:=DE01_+DE12_+DE23_;DS0123atm_:=DS01atm_+DS12atm_+DS23atm_:'DS0123atm'=evalf(%,2);DS0123air_:=0;#subs(SI2,SI1,DS01air_+DS12air_+DS23air_);

g)  Determinar la posición más cercana al fondo que llegaría a alcanzar el émbolo.

>	eqBE:=m*c[v]*T1*(T4/T1-1)=p0*V1*(1-V4/V1);x4_:=fsolve(subs(dat,SI0,m*c[v]*T1*((x1_/x4)^(gamma-1)-1)=p0*V1_*(1-x4/x1_)),x4=0..0.3)*m_;V4_:=subs(dat,x4_*A);p4_:=subs(dat,p1*(x1_/x4_)^gamma):p4=evalf(%/(1000*Pa_/kPa_));T4_:=subs(dat,p4_*V4_/(m*R));

i.e. el émbolo llega a acercarse hasta 0,26 m del fondo, comprimiéndose hasta 135 kPa y alcanzando 341 K.

>