| > | restart:#"m02_p03" |
Se trata de aplicar el concepto estadístico de entropía a una distribución de probabilidades continua, usando como por ejemplo la renta de una población. Se pide:
a) Calcualar la distribución más probable de la renta de una población.
b) Calcular el porcentaje de ricos (que ganan más que la media) y su porcentaje global de la renta total.
Datos:
En ausencia de mejor información, se supondrá que la renta o salario, s, es una variable conrinua que va de 0 a infinito, y que existe un valor medio, s0.
a) Calcualar la distribución más probable de la renta de una población.
Sea pds el porcentaje de la población con sueldo comprendido entre s y s+d
| > | eqN:=Int(p(s),s=0..infinity)=1;eqS:=Int(-k*p(s)*ln(p(s)),s=0..infinity)=S;eqE:=Int(s*p(s),s=0..infinity)=s0;Phi:=subs(p(s)=p,lhs(eqS+lambda*eqN+mu*eqE)); |
| > | eq0:=diff('Phi',p)=0;eq0_:=diff(subs(infinity=s,Phi),s);p_:=solve(eq0_=0,p); |
| > | eqN_:=subs(p(s)=p_,eqN);assume(k>0,mu<0,lambda>0);eqN_:=value(expand(eqN_));eqE_:=subs(p(s)=p_,eqE);eqE_:=value(expand(eqE_)); |

| > | ### WARNING: allvalues now returns a list of symbolic values instead of a sequence of lists of numeric values
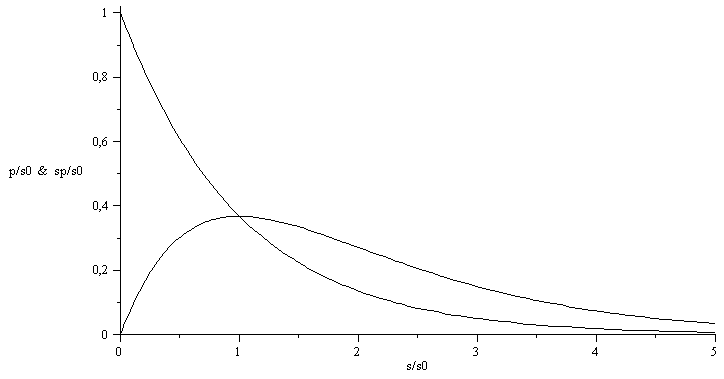
sol1:=combine(allvalues(solve({eqN_,eqE_},{lambda,mu})));p__:=expand(subs(sol1,p_));plot([subs(s0=1,p__),subs(s0=1,s*p__)],s=0..5,colour=black,labels=[`s/s0`,`p/s0 & sp/s0`]); |
 |
b) Calcular el porcentaje de ricos (que ganan más que la media) y su porcentaje global de la renta total.
Conclusión: el porcentaje de población con sueldo inferior al valor medio es del 63%.
| > | Int(p__,s=0..s0)=evalf(int(p__,s=0..s0),2);Int(p__*s,s=0..s0)=evalf(int(p__*s,s=0..s0),2); |
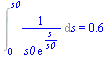 |
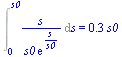 |
Conclusión: el porcentaje de población con sueldo inferior al valor medio es del 63% (el de ricos 37%) y sin embargo ese 63% de la población sólo dispone del 26% de la renta (y los ricos del 74%).
Nótese que, aunque se ha hecho este ejercicio pensando en las rentas para hacerlo más atractivo, es enteramente aplicable, por ejemplo, a la distribución de energías moleculares, como se puede ver en el problem siguiente, obteniéndose el mismo resultado: en un gas ideal en equilibrio la temperatura es proporcional a la energía cinética media de las moléculas, pero no todas las partículas tienen la misma energía (no es probable), sino que las energías cinéticas se reparten exponencialmente, como las rentas.
| > |